| CS-534: Packet Switch Architecture
Spring 2007 |
Department of Computer Science
© copyright: University of Crete, Greece |
1.1 Parallel and Serial Links, Rate, Throughput Conservation and Buffering
|
[Up - Table of Contents] [Prev - 0. Central Issues] |
[printer version - PDF] [1.2 Elastic Buffers - Next] |
Switching, interconnections, and networking is about
moving (digital) information around, from place to place.
Such movement can physically occur via wireless communication,
optical fibers, or metallic (usually copper) cables.
The highest performance interconnects
--the most challenging ones for switch architectures--
use optical fibers or metallic cables.
Transmission of information in these media can be modeled as follows,
at an abstraction level that suffices for the purposes of this course.
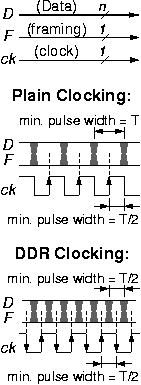
1.1.1 Parallel Transmission Links
Parallel transmission links, as illustrated in the figure, use multiple (n>1) conductors to carry an entire word --rather than a single bit-- in each unit of time. Parallel links are the customary form of interconnection in the datapath of processors and other digital systems: single-bit timing and control signals instruct the datapath how to process all n bits of the data at once. For the link to be usable at low cost, all bits of the word are synchronous to a given clock, ck. Usually, the need arises for one or more framing wires, F, to accompany the data of the link, in order to delineate cell or frame or packet boundaries; examples include signals to indicate valid/idle link word, or start_of_packet / end_of_packet, or header/body differentiation, etc. In a datapath terminology, framing information can be thought of as part of either data or control, depending on its encoding and its use. If the normal network traffic carried over the data wires does not use all 2n combinations of the n bits, then in-band signaling can be used, and the framing information can be carried over the data wires themselves, as control words, encoded using the n-bit combinations that remain unused by normal network traffic. Otherwise, when all bit combinations are acceptable values inside the network traffic, or when convenience or robustness dictates it, out-of-band signaling is used and separate framing wire(s) are included with the link. When n is large, the "overhead" cost of distributing the clock to all users of the link and of carrying the framing information on separate wires is small relative to the cost of the data wires themselves.When the clock frequency of a link is below the limits of technology for the driver circuits and the transmission line, plain, conventional clocking is used, as illustrated in the upper part of the figure, and as customary in ordinary digital systems employing edge-triggered flip-flops and registers: the link carries (up to) one word per clock cycle. If, however, the clock frequency is at the upper limits of technology, the following problem arises with conventional clocking: the pulse width on the clock wire is half as short as the shortest pulse width on the data wires, because the clock transitions twice per cycle, as compared to once per cycle for the data. That means that either the clock wire operates at technology limits --but then there is room for the data wires to operate faster-- or else the data wires operate at technology limits --but then it becomes impossible to send such a fast clock signal. To rebalance the signaling rate used on the two kinds of wires, Double Data Rate (DDR) Clocking is used: the link carries one word during the positive edge (or pulse) of the clock, and a second word during the negative edge (or pulse) of it. DDR clocking became popular with the recent generations of synchronous dynamic RAM (SDRAM). If f is the clock frequency (measured e.g. in MHz), then the signaling rate on the wires (measured in MBaud) is f for conventional clocking and 2f for DDR clocking; the transmission rate or link throughput (measured in Mbits/s or Mb/s or Mbps) is f·n for conventional clocking and 2f·n for DDR clocking (if the framing wire is included in the count, the transmission rate becomes f·(n+1) or 2f·(n+1), respectively).
In modern high-performance switching systems,
parallel links are used extensively inside ASIC chips,
and in few cases between nearby chips,
usually on the same printed circuit board (PCB).
The primary limitation of high-speed parallel links is
timing skew among the n cables making up the link.
As clock frequency increases,
when the bit-time gets so short as to be comparable to link skew,
synchronization among the bits of a word is lost,
and the link becomes unusable in the simple way outlined above;
Skew increases with link length,
when the link goes through connectors,
and with link width (the number of wires, n+2 or so);
clock distribution may also introduce clock skew,
which adds to the data skew.
When skew becomes severe,
e.g. in chip-to-chip links operating at several hundred MHz frequencies,
two methods are used to alleviate it:
(i)
Source-Synchronous Clocking:
instead of distributing the clock from a central location
to the driver and to the receiver of the link,
the link driver (source) sends the clock along with the data,
through similar driver circuits and parallel (same length) PCB traces,
to the receiver;
in this way, the clock delay becomes comparable to the data delay,
and skew among them is reduced; and
(ii)
Partial-Word Clocking:
when the link is very wide (e.g. 32 or 64 bits),
a separate, source-synchronous clock signal is sent
along with every --e.g.-- 8 or 16 of the data wires;
wire overhead stays low (1/8th or 1/16th),
while skew is reduced within each separate 8-bit or 16-bit sub-link.
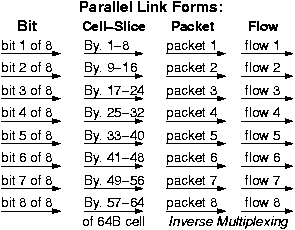
Other Forms of Parallelism, Inverse Multiplexing
Parallelism is the primary means to achieve high performance in interconnects, as in most other domains, too. The form of parallelism seen above can be called bit-level parallelism, and makes sense when all the wires of the link operate in synchrony with a single clock. At higher rates or longer distances, when such synchronous operation cannot be maintained, the individual wires in the link behave more like separate, independent sub-links. Then, it becomes more natural to distribute the data over the sub-links not on a bit-by-bit basis but at coarser granularity: bytes, or cell-slices, or packets, or flows, as illustrated in the figure, here.
Packet-level and flow-level parallelism is especially interesting, and has some important differences from fine-grain parallelism: while all bits of a word and all slices of a cell can be shipped at about the same time over all sub-links, all packets may not be available at the same time, and all flows may not present the same load to the network. Inverse Multiplexing is the general term used to describe these other forms of parallelism, and especially the coarse-grain ones: packet-level and flow-level. As will be seen in the chapter on switching fabrics, inverse multiplexing is the primary technique to achieve trully scalable high-performance switching.
1.1.2 Serial Transmission Links
Serial transmission links carry all of their information through a single line --electrical conductor or optical fiber (the electrical conductor normally uses two wires, in the form of coaxial cable or twisted pair). In the old times, at low signaling frequencies, the primary reason for using a single line was cost reduction. Currently, in the Giga-Hertz era, where bit times are shorter than a nanosecond, the primary reason is that the inevitable timing skew between any two signals carried over a distance longer than a meter or so exceeds the bit time duration. Thus, for long and fast links, it is impossible to maintain synchronization, not only among multiple data bits, but even between one data and one clock wire. Consequently, the receiver is forced to extract the clock from the single serial signal received over the single line. For long distances, even when cost is not an issue and we use multiple parallel lines for performance reasons ("other forms of parallelism", above) (e.g. multiple fibers or multiple wavelengths in one fiber - WDM), the simple clocking scheme of parallel link (§1.1.1) cannot be used --the receiver is forced to extract a separate, individual clock from each and every one of the multiple parallel conductors.
The functions typically present in a serial line receiver
are illustrated in the block diagram:
clock recovery, serial-to-parallel conversion, and framing recovery.
The incoming serial data waveform
may stay at high or low voltage for long time intervals,
corresponding to trains of cosecutive 1's or 0's.
For correct reception, we need to know the signaling rate
to a certain degree of accuracy,
related to the length of the longest sequence of 1's or 0's.
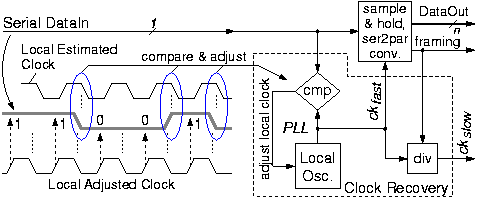 Clock recovery begins with a local oscillator
whose frequency is approximately equal to the known signaling rate.
Next, the exact frequency and phase of this oscillator
must be adjusted to match the incoming serial signal,
using a phase-locked loop (PLL):
whenever an edge occurs on the incoming serial data,
the timing of that edge is compared to the phase of the oscillator;
if a systematic bias is detected for a certain length of time,
the local oscillator phase is adjusted to compensate for that.
The end result, when transmission quality is good enough
(low phase jitter on the serial data),
is that the phase of the local oscillator remains "locked"
to the transitions of the incoming serial signal,
thus forming the recovered clock, ckfast.
The other edge of this recovered clock
--the edge that falls at the middle between signal transitions--
is then used to sample the incoming signal,
latching and holding the received data;
in the figure, the data being received is "11001".
Clock recovery begins with a local oscillator
whose frequency is approximately equal to the known signaling rate.
Next, the exact frequency and phase of this oscillator
must be adjusted to match the incoming serial signal,
using a phase-locked loop (PLL):
whenever an edge occurs on the incoming serial data,
the timing of that edge is compared to the phase of the oscillator;
if a systematic bias is detected for a certain length of time,
the local oscillator phase is adjusted to compensate for that.
The end result, when transmission quality is good enough
(low phase jitter on the serial data),
is that the phase of the local oscillator remains "locked"
to the transitions of the incoming serial signal,
thus forming the recovered clock, ckfast.
The other edge of this recovered clock
--the edge that falls at the middle between signal transitions--
is then used to sample the incoming signal,
latching and holding the received data;
in the figure, the data being received is "11001".
Obviously, for clock recovery to be successful, the incoming serial signal must transition between 0 and 1 at least once every given number of clock periods (bit intervals). In other words, the maximum length of trains of cosecutive 1's or 0's must be bounded; this bound is related to the phase jitter of the signal and to the frequency difference between the transmitter and receiver oscillators. If arbitrary (binary) user data are transmitted, this requirement may not be satisfied, --e.g. when a long sequence of null bytes (or FF or -1 numbers) is being sent. To cope with that, proper line coding schemes are used, which introduce a certain proportion of redundancy or overhead information to ensure that signal transitions will occur often enough. A popular line code, used in Fibre Channel and Gigabit Ethernet, is the 8B/10B encoding, which encodes each 8-bit byte using a 10-bit codeword (even though capital, the B's in this name mean "bit", not "byte"!). 8B/10B encoding provides for simple encoder and decoder circuits, and is robust in terms of oscillator and channel (jitter) quality, at the expense of a high proportion of overhead bits relative to data: 25 percent (%). Another popular line code is SONET (Synchronous Optical Network); it uses just around 3.5 % of overhead bits, but requires better quality of channel and more expensive transmitters and receivers.
Line Codes and Framing:
The next problem after clock recovery is Framing: how to discover the boundaries of bytes and cells/frames/packets in a long series of bits, in the lack of additional information. If these boundaries are found once, i.e. if frame synchronization is achieved once, then, in theory, the system would be able to maintain such synchronization forever: byte boundaries are found by counting bits (eight-by-eight); cell or frame boundaries are found by counting bytes (modulo the fixed, known cell or frame size); and for variable-size packets, their boundaries are found by looking at the packet size field in the header of each packet to determine where this packet ends, hence where the next packet begins, thus where that next packet's header and size field are, etc. However, a practical system must operate robustly in the presence of noise and bit errors (including burst errors), hence in the presence of occasional losses of bit and/or frame synchronization. Thus, the line coding scheme must be properly designed in order to enable the receiver to recover frame synchronization after occasional loss of it.
Line codes achieve the two above goals using the following general idea. Take the 8B/10B encoding as an example. For each data byte, a 10-bit codeword is transmitted. There are 1024 different codewords. Out of them, we must select 256 codewords to represent the 256 different data byte values, plus a few more codewords to represent some control characters intended for out-of-band signaling purposes. The rest of the 1024 existing codewords will be "banished" as illegal. First, banish those codewords whose bit representation contains too few 0-1 or 1-0 transitions, i.e. which contain sequences of 1's or 0's that are too long. Second, banish the codewords that, when placed adjacent to other, legal codewords would result in too few transitions at the boundary between the two codewords (i.e. a suffix of one word and a prefix of the other would form a sequences of 1's or 0's that is too long).
Next, choose a codeword, called SYNC, that is appropriate as a synchronization control character; SYNC characters are to be transmitted periodically in order for the receiver to use them when it needs to recover byte and frame synchronization. When synchronization is lost (as detected by too high of an error rate), the receiver examines all groups of 10 bits, starting at every arbitrary bit position, looking for a SYNC character; when found, the SYNC character indicates byte boundaries, and it may also indicate cell or frame or packet boundaries. Hence, the SYNC bit pattern must never appear at the boundary of two legal codewords, i.e. a suffix of one legal codeword and a prefix of another must never form the SYNC bit pattern. Finally, choose the required legal codewords (256 data byte values plus possibly a few more control characters) among the remaining codewords so as to maximize the Hamming distance among legal words, in order for the code to possess good error detection properties (the Hamming distance between two codewords is the minimum number of bit inversions required to transform one of them into the other).
Control characters, as described above, are legal codewords that are distinct from the 256 data byte values, and thus can be used for out-of-band signaling, i.e. to convey information --even in the middle of cells/frames/packets-- that is not part of user headers or payload. The SYNC character, as seen above, is one such control character. Other control characters may be intended for flow control (backpressure) --e.g. XON/XOFF: start/stop transmission. When no useful data exist to be transmitted over the link, a special control character must be transmitted instead --this can be SYNC, or it can be another bit pattern, e.g. called IDLE.
Returning to the typical block diagram, in the figure above, the received data must be converted to parallel form and decoded from the line code to plain, unencoded values. Serial to parallel conversion is usually done in order to reduce clock frequency, because serial link transmission rate is usually quite higher than ASIC clock frequencies. Other reasons include decoding from the line code, and the usual form of on-chip processing in parallel rather than serial datapaths. The following subsection defines various rate and throughput terms, and describes throughput relationships. Then we discuss conversions between serial and parallel data formats.
Signaling Rate, Transmission Rate, Throughput, Capacity, and Load:
The Signaling Rate of a line (electrical conductor or fiber) is the number of data symbols that the line carries per unit of time, where each symbol is carried "at once" --without the line transitioning from one value to another while the symbol is being transmitted. The signaling rate is measured in Baud. For the parallel link of §1.1.1 operating with a clock frequency f, the signaling rate is f for conventional clocking and 2f for DDR clocking. For the serial link of §1.1.2, the signaling rate is equal to the frequency of the recovered (fast) clock, ffast .
The Transmission Rate of a link is the number of raw bits that it carries per unit of time; hence, the transmission rate is equal to the signaling rate times the number of bits per symbol. The transmission rate is measured in bits/s or b/s or bps. Some communication links --not in our course-- carry digital non-binary symbols; for example, if each symbol is a quantity (e.g. voltage) with 4 distinct acceptable values, then that link carries 2 bits per symbol. For the n-wire parallel link of §1.1.1, each symbol is an n-bit word, ignoring the framing wire, or an (n+1)-bit word if we include the framing wire; thus, its transmission rate is f·n or 2f·n, --without the framing bit, for plain or DDR clocking respectively-- or f·(n+1) or 2f·(n+1) when the framing wire is included in the count. For the serial link of §1.1.2, each symbol is one bit, and its transmission rate is ffast .
The Throughput of a link is the number of useful bits that it carries per unit of time; we can say that Throughput equals Transmission Rate minus Overhead. The definition of useful bits versus overhead is context-dependent, and so is the definition of throughput. For the parallel link of §1.1.1, if we assume that the n data wires carry useful information versus the overhead carried by the framing wire, then throughput is f·n, as contrasted to the transmission rate of f·(n+1) (for plain clocking). For the serial link example with the 8B/10B line code seen in §1.1.2, throughput is eight tenths (8/10) of transmission rate. However, depending on context, additional bits may be considered overhead. For example, in Gigabit Ethernet links, consecutive packets must be separated by a 12-byte (minimum) interframe gap, and each packet must be preceeded by an 8-byte preamble; these are additional types of overhead, further reducing the actual "user" throughput. In some contexts, it may also be appropriate to consider encapsulation headers as overhead.
The words "throughput" or "rate" may refer
to the Peak Capacity of the link,
or to the Current (instantaneous or average) Load
actually present on the link.
Peak capacity refers to when the link carries
as much user information as possible per unit time
("back-to-back packets");
at other periods,
the actual load on the link may be less than peak capacity,
because less user traffic is available for transmission,
thus leaving idle periods between packets.
Again,
the interpretation of "throughput" or "rate" is context-dependent.
For clarity, it is preferable to use the term "(peak) capacity"
to refer to the maximum throughput of the link,
or the term "(current) load" to refer to the actually present traffic.
The single word "throughput" usually refers to link capacity,
while the single word "rate" sometimes refers to link load,
especially in the context "traffic rate" or "flow rate".
Load can be measured in bits/s, like throughput,
but it is also often measured
as a fraction or percentage of peak capacity
--e.g. "load=0.8" or "80% load".
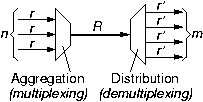
1.1.3 Throughput Conservation, Buffer Space, Delay
At the core of things, switching consists of a large collection of devices where information from multiple sources is aggregated onto a single link (called multiplexing), or information from a single link is distributed to multiple destinations (called demultiplexing), or both at the same time. The first metric to consider at such points is throughput: under one or another of the definitions discussed above, throughput is conserved across these aggregation or distribution points. In the case of the figure, where the n incoming links have a throughput of r each and the m outgoing links have a throughput of r' each, the aggregate incoming throughput is n·r, and this must be equal to the throughput R of the shared link, and to m·r', the aggregate departing throughput: n·r = R = m·r'.The exact definition for throughput to be used in this conservation equation depends on the kind of processing performed between lines. In the simplest case, the totality of raw bits are transferred from input to output, not dropping or adding any overhead information (hence no memory is needed other than sample-and-hold flip-flops). In this case, transmission rate is conserved across the conversion point.
In other cases, code conversion or packet translation takes place: one protocol's overhead is dropped from the incoming traffic, and another protocol's overhead is added to the outgoing stream; however, the useful bits are preserved from input to output. Alternatively or at the same time, idle periods may be squeezed out of the incoming line, with new, different idle periods added to the outgoing stream; idle periods are transmitted when no useful traffic exists to be sent, or when it is not appropriate to send traffic due to flow control (policing, shaping, backpressure, etc). Also, filtering out or dropping some incoming packets, e.g. because they are destined elsewhere, is equivalent to treating them as idle periods. In all such cases, throughput is conserved, where throughput is defined based on which useful bits are carried intact from input to output.
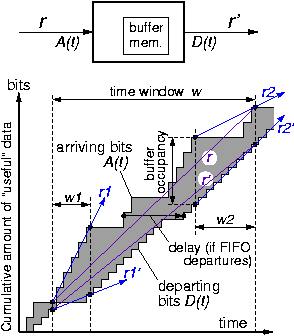
For all these reasons, instantaneous (useful bit) throughput may be much below peak line throughput (capacity), and may also differ a lot from average throughput. To smooth out the fluctuations in instantaneous throughput, possibly adjusting the traffic to a different-capacity line or to a different flow control scheme or domain, Buffer Memory is needed in order to be able to vary the departure time of each bit (packet) relative to its arrival time, as illustrated in the figure.
Let A(t) be the function that describes
the arrival of useful bits,
while D(t) describes their departure.
These are both monotonically increasing functions of time,
equal to the cumulative number of useful bits
that have flown through the respective interface
since the beginning of time;
"useful" bits are the bits that are preserved from input to output,
across whatever processing the node performs.
Because of causality (no bit can depart before its arrival),
D(t) never exceeds A(t), at any given time t.
The difference A(t)-D(t) equals
the number of bits that have arrived but not yet departed
at time t;
these bits are necessarily stored in the buffer memory,
hence A(t)-D(t) equals
that buffer memory occupancy at time t.
The slope of A(t)
is the rate of useful bit arrival,
hence it equals the incoming throughput;
similarly, the slope of D(t) equals the outgoing throughput.
At the clock cycle granularity,
information arrival and departure is quantized,
so A(t) and D(t) are step functions;
if line capacity (peak throughput) is one word per cycle,
then each step equals one word
--the figure was drawn assuming that word size on the input side
is twice the word size on the output interface.
At coarser time granularity,
we can approximate A(t) and D(t) as smooth functions.
Slope (throughput) is then approximated
over a suitable time window:
let w be the window from time t to time t+w;
over that window,
the incoming useful-bit rate (throughput) r
and the outgoing rate r' are:
Assume that buffer occupancy, A(t)-D(t), never exceeds B, at any time t, because flow control appropriately adjusts rates r and r'; if B is the size of the buffer memory, then this is the rate adjustment necessary for the memory not to overflow, hence for useful information not to be lost. Since A(t+w)-D(t+w) is non-negative and does not exceed B, and since the same is true for A(t)-D(t), then their difference |(A(t+w)-D(t+w)) - (A(t)-D(t))| is bounded above (in absolute value) by B. This latter difference can be rewritten as |(A(t+w)-A(t)) - (D(t+w)-D(t))|, which is equally bounded by B. Diving by w, the time window, we get |(A(t+w)-A(t))/w - (D(t+w)-D(t))/w|, which is equal to |(r-r')|, the difference between the average incoming and outgoing rates. We can then express the bound in the following forms, which we discuss in the next few paragraphs:
The throughput difference, |r-r'|, averaged over w, is no more than (B/w); or:
The buffer memory, B, is at least |r-r'|·w
(Avg. Buffer Occupancy) · (w) = (Avg. Delay) · (Traffic Volume)
Traffic volume (number of bits) equals throughput (r or r', since they are equal to each other in the long run) multiplied by the length of the time window w. Dividing both terms of the equation by the traffic volume, expressed as r·w or r'·w, we get:
Average Delay = (Average Buffer Occupancy) / r (or divided by r')
We can view the buffer memory as a slow-down pipe
of length b,
where b is the average buffer occupancy.
When a byte enters the pipe,
it finds b other bytes in front of it;
they have to depart at rate r' before "our" byte can depart,
and it will take them b/r' time to depart,
so "our" byte will be delayed by that much.
Alternatively,
between the time "our" byte arrives (being last in the queue)
and the time it departs (being first in the queue),
a queue of length b will build up behind it
due to new bytes arriving at a rate r;
the time for this queue to build up is b/r,
so this is the delay of "our" byte.
1.1.4 Parallel-to-Serial Conversion: Multiplexing
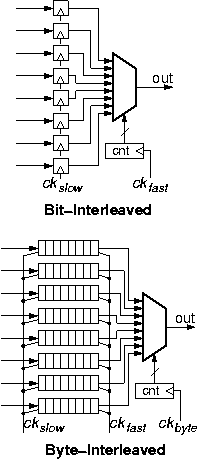
Parallel links (§1.1.1) carry information on multiple wires, while serial links (§1.1.2) serially transmit all information bits on a single wire. Conversion of a link from the former to the latter type is performed with the simple circuit shown in the upper part of the figure. Given the law of throughput conservation (§1.1.3), which in this case applies to the raw bits (transmission rate) of the links, the signaling rate ckfast on the serial link must be n times higher than the signaling rate ckslow on the parallel side, where n is the width of the parallel link (in the figure, n=8). The main digital component to perform the conversion is the multiplexor circuit: it circularly selects each one of the n bits of the parallel word, placing them on the serial line, for one clock period of the fast clock each; thus, during each period of the slow clock (= n periods of the fast clock), the multiplexor places all n bits on the serial line, one after the other, and is then ready to do the same with the bits of the next word during the next period of the slow clock. Note the similarity of this circuit to an 8x1 memory, where all 8 locations are written in parallel, but reading is sequential, one location at a time, circularly reading from the 8 addresses; also, note the equivalence to a parallel-in/serial-out shift register. Buffer memory is not needed because transmission rates do not fluctuate. The amount of (flip-flop) storage is limited to one (8-bit) word because the worst-case delay (last bit in each word) equals one word time (one slow clock period).The multiplexor circuit is used every time information from multiple source wires must be (selectively) placed onto a single output wire. As discussed in §1.1.1, multiple wires often carry traffic at various degrees of granularity --different bits of one word, or different bytes of a cell, or different packets of a flow, or different flows. The portions of traffic on each wire may be related to each other to a higher or lower degree: when individual bits are carried, they belong to a same word; when different flows are carried, however, they may be quite unrelated to each other, with the only common characteristic being that they share a common path through the network. The lower part of the figure illustrates a case where multiplexing is used to aggregate such coarser-grain information from eight incoming to one outgoing link. In such cases, it is customary to interleave the information on the shared link not on a bit-by-bit but on a coarser granularity; as we will see soon, this allows operation with wider buffer memories, hence at higher throughput.
The example labeled "byte-interleaved" in the figure
illustrates a case where multiplexing is on a byte-by-byte basis,
as in digital telephony (§2.1).
Again, for throughput conservation,
the signaling rate ckfast on the output link
must be n=8 times higher than
the signaling rate ckslow on the input links.
The output link, now, must carry
all 8 bits of a byte from the first link,
then all 8 bits of a byte from the second link, and so forth,
rather than 1 bit from each link.
When the 8 bits of a byte are transmitted on the output,
they must be transmitted at the fast clock rate;
however, these same 8 bits arrive through their input
at the slow clock rate,
and thus the arrive during a time interval n=8 times longer
than the interval in which they must depart.
To equalize the instantaneous rate difference
at the byte level of granularity,
a buffer of size one byte is needed per incoming line
(§1.1.3).
The figure schematically illustrates each such buffer
as a horizontal array of 8 flip-flops,
which we imagine as being filled from the left using the slow clock,
and as emptying to the right using the fast clock
(filling occurs during all slow-clock periods;
emptying occurs during 8 consecutive
out of every 64 fast-clock periods).
The physical implementation of this buffer
may be a dual-ported register (flip-flop) file,
or two shift registers using the double-buffering concept
(shift-in to the first register at the slow-clock rate,
then transfer all 8 bits in parallel to the second register,
then shift-out of that second register at the fast-clock rate).
Notice that the multiplexor now has to switch selections
at a slower rate: once every byte time on the fast link,
rather than once every bit time in the bit-interleaving configuration.
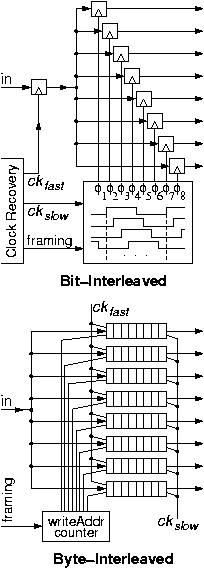
1.1.5 Serial-to-Parallel Conversion: Demultiplexing
In the previous section, 1.1.4, we saw that parallel-to-serial converters resemble a memory with multiple, parallel (slow) write ports and one sequential (fast) read port, used to circularly read the memory. The central component was a multiplexor, used to aggregate information from multiple sources to one destination. Serial-to-parallel is the reverse conversion, and it is based on demultiplexing, that is distributing information from one source to multiple destinations. Not surprisingly, the demultiplexor, shown in the figure, looks like a memory with one sequential (fast) write port, circularly writing into all memory locations, and multiple, parallel (slow) read ports, reading from all memory locations.In the bit-interleaved version, the incoming serial link carries frames of n bits containing 1 bit for each of the n parallel outputs (n=8 in the figure). Each bit of the frame is latched into one of the n=8 flip-flops, clocked by the appropriate phase, ö1 through ö8, of the slow clock. As in the previous section, one period of the slow clock equals n=8 periods of the fast clock; each phase differs from the next by one fast-clock period, i.e. by one bit time on the serial link. The net effect of the 8 phases is to circularly write into the 8 flip-flops of the 8x1 memory, in a way analogous to the circular reading (using a counter to drive the multiplexor) in the previous section (1.1.4). The proper alignment of ö1, so that it picks the first bit of each frame, is based on framing information that has to be extracted from the overhead bits of the serial link by the clock recovery circuit (§1.1.2).
In the byte-interleaved version,
incoming frames contain n=8 bytes each.
All 8 bits of a byte arrive contiguously in time
and are destined to one of the output links.
These 8 bits must be written
into the proper word (byte) of the 8x8 memory,
at the rate of the fast clock at which they arrive;
on the output side, they are read out at the slow clock rate.
Writing into each word (byte) of the 8x8 memory
is enabled for 8 out of the 64 (fast) clocks of each frame;
selection of the proper 8 of the 64 clocks
is based on framing information, as above.
Again, the net effect is to sequentially and circularly write
into the memory,
while on the read side the n ports operate in parallel
but at an n times slower rate.
|
[Up - Table of Contents] [Prev - 0. Central Issues] |
[printer version - PDF] [1.2 Elastic Buffers - Next] |
| Up to the Home Page of CS-534
|
© copyright
University of Crete, Greece.
Last updated: 11 Mar. 2007, by M. Katevenis. |