| CS-534: Packet Switch Architecture
Spring 2013 |
Department of Computer Science
© copyright: University of Crete, Greece |
Exercise Set 9:
TST and Clos Circuit Switch Scheduling
Assigned: 2 May 2013 (should be week 9) -
Due: Mon. 27 May 2013 (week 12 - should be 11)
| [Lectures: 1. TST Ckt Sw, 5. Fabric Topologies] | [print version, in PDF] |
 9.0
TST and Clos Switch Scheduling
9.0
TST and Clos Switch Scheduling
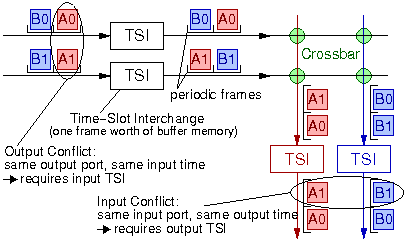
In chapter 1,
slide 15 (also shown here on the right),
we discussed the need for time-slot interchanges (TSI)
in front of the crossbar, in a time-space-time (TST) circuit switch,
in order to rearrange the position of the various connections
inside the (synchronized) incoming frames,
so as to eliminate output contention in the crossbar
(i.e. no two connections in similar positions --same time--
of two different frames have the same outgoing link).
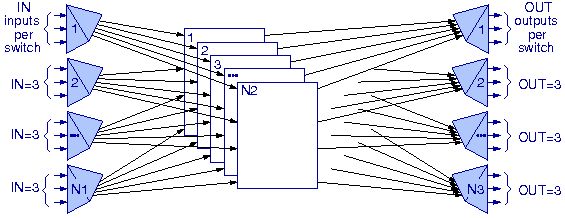
In §5.2.3,
slide 23 (also shown below on the right),
we saw the 3-stage Clos network
(and, before that, its specialization, the Benes network).
 There is an analogy --or even equivalence--
between these two systems in circuit switching
(the analogy carries over to packet switching,
with TST becoming an input-queued or CIOQ crossbar,
and Clos becoming a "Parallel Packet Switch" (PPS)).
The analogy goes as follows.
Each of the Clos middle-stage switches
implements one time slot of the TST crossbar inside a frame;
there are N2 middle-stage switches in the Clos network,
and there must be N2 time slots
in each frame of the crossbar in the TST switch.
The role of each input TSI in the TST is to "switch" in time any connection,
from the arbitrary time slot that it arrives at,
to an arbitrary time slot when the crossbar is available to serve it;
correspondingly, the role of each first-stage switch in the Clos
is to switch "in space" any connection,
from the arbitrary input port that it enters on,
to an arbitrary middle-stage switch that is available to serve it.
The general Clos fabric has N1 first-stage switches,
each of them of size INxN2;
and there are N2 middle-stage switches,
each of them of size N1xN3.
The corresponding TST system has N1 input TSI's
--one for each of the N1 input ports of the crossbar;
each input TSI receives a frame consisting of IN time slots,
and arbitrarily rearranges its contents
placing them into a frame consisting of N2 time slots;
the crossbar is of size N1xN3
and is shared among the N2 time slots in its frame
(reconfigured N2 times per frame).
Output TSI's in TST play a role
corresponding to the third-stage switches in Clos,
in a way analogous to input TSI's and first-stage switches.
There is an analogy --or even equivalence--
between these two systems in circuit switching
(the analogy carries over to packet switching,
with TST becoming an input-queued or CIOQ crossbar,
and Clos becoming a "Parallel Packet Switch" (PPS)).
The analogy goes as follows.
Each of the Clos middle-stage switches
implements one time slot of the TST crossbar inside a frame;
there are N2 middle-stage switches in the Clos network,
and there must be N2 time slots
in each frame of the crossbar in the TST switch.
The role of each input TSI in the TST is to "switch" in time any connection,
from the arbitrary time slot that it arrives at,
to an arbitrary time slot when the crossbar is available to serve it;
correspondingly, the role of each first-stage switch in the Clos
is to switch "in space" any connection,
from the arbitrary input port that it enters on,
to an arbitrary middle-stage switch that is available to serve it.
The general Clos fabric has N1 first-stage switches,
each of them of size INxN2;
and there are N2 middle-stage switches,
each of them of size N1xN3.
The corresponding TST system has N1 input TSI's
--one for each of the N1 input ports of the crossbar;
each input TSI receives a frame consisting of IN time slots,
and arbitrarily rearranges its contents
placing them into a frame consisting of N2 time slots;
the crossbar is of size N1xN3
and is shared among the N2 time slots in its frame
(reconfigured N2 times per frame).
Output TSI's in TST play a role
corresponding to the third-stage switches in Clos,
in a way analogous to input TSI's and first-stage switches.
In this exercise set we will study the way in which the input TSI's in a TST circuit switch should rearrange the incoming connections. To make it easier to think about the problem, we will formulate it using colors, as in the next figure. Colors, in our case, will correspond to outgoing links; in the figure there are n=4 outgoing links, so there are n=4 colors. For simplicity we will assume that the number of incoming links is also n, equal to the number of outgoing links, and that all liks have the same speed, hence the same number of slots in their frames --call this number m.
Let us call "crossbar schedule" the colored rectangular array shown in the figure; in this array, the horizontal direction corresponds to time (slots in a frame), the vertical direction corresponds to crossbar inputs, and the color corresponds to crossbar outputs, as discussed above. Our topic is the construction of this schedule; once the "schedule" is set, we know how to configure the crosspoint of the space switch during each time slot of the frame. The schedule corresponds to the frames produced by the input TSI's. Once the schedule is constructed, setting the TSI's so as to generate it is straightforward, so we will not discuss that here. Also, assigning specific connections (circuits) to specific entries in the schedule can be done in any random way, as long as an entry of the correct color (output) is used in the correct row (input) of the table. Thus, for our purposes here, all entries of the same color in the same row of the schedule are completely equivalent to each other and interchangeable. We can now formulate the inputs to our problem, and the constraints that the solution sought must satisfy.
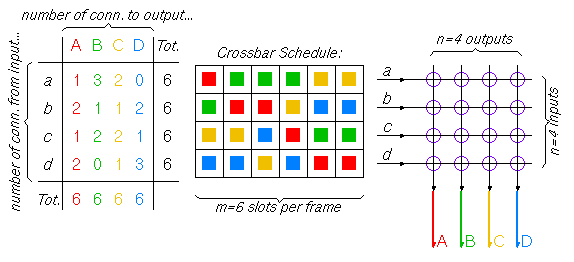 For a given switch size n and frame size m,
the input to our problem is the n x n array of numbers
shown in the left of the figure.
Each entry in this array specifies
the number of connections (circuits) on a given incoming link
to be switched onto a given outgoing link.
Obviously, the sum of the numbers in each row
(the total number of circuits on an incoming link)
cannot exceed m (the frame size);
similarly, the sum of the numbers in each column
(the total number of circuits on an outgoing link)
cannot exceed m.
In one sense,
the problem of schedule construction is hardest
when the schedule is full, as in the figure,
i.e. when all these horizontal and vertical sums
are equal to m
(in another sense, constructing a full schedule has some advantages
--see exercise 9.3 below).
The problem to be solved is the construction of a schedule
for the given numbers of connections.
A schedule is an n x m array of colors, as shown above,
that satisfies the following constraints:
For a given switch size n and frame size m,
the input to our problem is the n x n array of numbers
shown in the left of the figure.
Each entry in this array specifies
the number of connections (circuits) on a given incoming link
to be switched onto a given outgoing link.
Obviously, the sum of the numbers in each row
(the total number of circuits on an incoming link)
cannot exceed m (the frame size);
similarly, the sum of the numbers in each column
(the total number of circuits on an outgoing link)
cannot exceed m.
In one sense,
the problem of schedule construction is hardest
when the schedule is full, as in the figure,
i.e. when all these horizontal and vertical sums
are equal to m
(in another sense, constructing a full schedule has some advantages
--see exercise 9.3 below).
The problem to be solved is the construction of a schedule
for the given numbers of connections.
A schedule is an n x m array of colors, as shown above,
that satisfies the following constraints:
- the number of entries of each color on each row are equal to the corresponding number of connections given; and
- each color appears at most once in each column of the schedule.
9.1 Schedule Rearrangement when adding new Connections
When adding new connections (circuits) to a (not fully utilized) switch, the crossbar schedule cannot always be updated by merely adding new entries to it --there are situations where existing entries in the schedule have to be rearranged. This corresponds to the "rearrangeably non-blocking" Clos networks.(a) To see this, construct the following small scenario. Consider a 3x3 switch (n=3) with a frame size of m=2. First, set-up a red connection on input a, then add a green connection on input b, and then another green connection on input c. Now, try various scenaria of adding more red or blue connections, in ways such that the new connections require or do not require rearrangement of the first three entries in the schedule.
(b) Can you modify your placement of the first three entries in the schedule of question (a) so that no new addition after that will require rearrangement?
(c) Make some scenaria similar to question (a) for a 3x3 switch (n=3) with a frame size of m=4.
This exercise 9.1 guides us to consider that algorithms for schedule construction should probably fall in one of two categories: either (i) the algorithm considers the connections in a random order, but then it must be prepared to rearrange schedule entries made earlier; or (ii) the algorithm must start with "global" knowledge of all connections to be made, and must then consider them in some particular "clever" order.
Next, we want to think whether a schedule always exists and work towards an algorithm for constructing a schedule for any given set of numbers of connections (that do not exceed line capacities), under the assumptions in this exercise set (equal number of crossbar inputs and outputs, equal frame size on inputs and outputs). This is a hard and beautiful problem, and it is worth thinking about it for a while.
9.2 Building a Schedule one Column at a Time
Let us try to construct a schedule one column at a time. In this exercise we will assume that the switch is fully utilized, i.e. the total number of connections per input as well as per output is equal to the frame size m. Under this assumption, all columns of the schedule must be full, which means that each column is "merely" a permutation of all n colors.
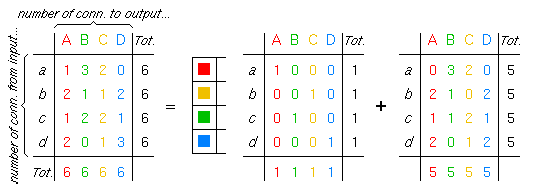 After one column of the schedule is built,
constructing the rest of the schedule is equivalent to
constructing a schedule for a switch with frame size m-1
and for a connection-number array
that results from the original array
after subtracting 1 from each entry that corresponds
to each of the colors and inputs that were included
in the first column that was built.
This is shown pictorially in the figure here,
and it is equivalent to decomposing the original connection-number array
into a sum of m "permutation" arrays
(arrays like the one in the middle of this figure).
After one column of the schedule is built,
constructing the rest of the schedule is equivalent to
constructing a schedule for a switch with frame size m-1
and for a connection-number array
that results from the original array
after subtracting 1 from each entry that corresponds
to each of the colors and inputs that were included
in the first column that was built.
This is shown pictorially in the figure here,
and it is equivalent to decomposing the original connection-number array
into a sum of m "permutation" arrays
(arrays like the one in the middle of this figure).
(a) Try to see whether this iterative algorithm will result in the construction of a valid schedule. A crucial point in to see whether it is always possible to find a full permutation of all colors in each and every step where a new column is built (without backtracking to rearrange previously made columns). Does it help to observe that the sums of the entries in the connection-number array, per row and per column, are all equal to m-i after the i-th step of the algorithm? Write your thoughts down, without spending an excessive amount of time to fully solve the problem.
(b) Think about, and discuss, various methods for constructing the permutations of colors that define the columns of the schedule during each step of the algorithm. Does it make a difference if you try to "consume" first the larger entries of the connection-number array, with the hope of ending up with few zero entries, or, conversely, if you try to consume first the smaller entries (the 1's), with the hope of ending up with many zero entries? Of course, a row or a column with a single non-zero entry immediately provides you with a uniquely-defined entry for the schedule, but does it also constrain you by making it harder to come up with the rest of the entries? Write your thoughts down, without spending an excessive amount of time to fully solve the problem.
9.3 Building a Schedule for a Non-Fully-Utilized Switch
Revisit exercise 9.1 in view of the algorithm developed in exercise 9.2. In exercise 9.1, connections were added to a non-fully utilized switch, and, as we saw, this necessitated, in some cases, the revision of the previously constructed schedule. The algorithm of exercise 9.2, on the other hand, assumed a fully-utilized switch.Make some proposal(s) on how to adapt the algorithm of exercise 9.2 to non-fully utilized switches. Does the new algorithm look easier or harder? Apply your new algorithm to the scenaria of exercise 9.1(a). Where exactly in the algorithm is the point where a decision is made based on an "assumption" about future connections, such that, if the "assumption" turns out to be false, the schedule will have to be rearranged when the actual new connections arrive? Write your thoughts down, without spending an excessive amount of time to fully solve the problem.
Bibliographic References:
The questions posed in exercises 9.2 and 9.3 are exciting, non-trivial problems. The following bibliographic references are related to them (you are not required to read them for answering this exercise set):- T. Inukai: "An Efficient SS/TDMA Time Slot Assignment Algorithm", IEEE Trans. Communications, vol. 27, Oct. 1979, pp. 1449-1455.
- I. Gopal, D. Coppersmith, C. Wong: "Minimizing Packet Waiting Time in a Multibeam Satellite System", IEEE Trans. Communications, vol. 30, 1982, pp. 305-316.
- M. Bonuccelli, I. Gopal, C. Wong: "Incremental Time-Slot Assignment in SS/TDMA Satellite Systems", IEEE Trans. Communications, vol. 39, no. 7, July 1991, pp. 1147-1156.
| Up to the Home Page of CS-534
|
© copyright
University of Crete, Greece.
Last updated: 2 May 2013, by M. Katevenis. |