| ΗΥ-120: Ψηφιακή Σχεδίαση
Φθινόπωρο 2007 |
Τμ. Επ. Υπολογιστών © Πανεπιστήμιο Κρήτης |
Εργαστήριο 5:
Δυαδική Αρίθμηση, Αθροιστές
5 - 8 Νοεμβρίου 2007
Διαγωνισμός Προόδου: Σάββατο 10 Νοεμβρίου 2007, 12:05 - 14:00
|
[Up - Table of Contents] [Prev - 4. Karnaugh, RAM] |
[printer version - PDF] [6. Signed Int., Subtr. - Next] |
[Βιβλίο (Wakerly): προαιρετικά μπορείτε να διαβάσετε τις παραγράφους 2.1 - 2.4 (σελίδες 31-40), και τις παραγράφους 5.10.1 - 5.10.2 (σελ. 508-510)].
Ασκήσεις 4.7 και 4.8 στην Άλγεβρα Boole
[Θυμηθείτε ότι θα παραδώσετε μαζί με την αναφορά σας αυτού του εργαστηρίου και τις απαντήσεις σας στις ασκήσεις 4.7 και 4.8 της προηγούμενης βδομάδας].5.1 Δυαδική Αρίθμηση:
Μία δυαδική λέξη αποτελούμενη από n bits μπορεί να αναπαραστήσει ένα από 2n διακριτά στοιχεία, με τη χρήση ενός κώδικα που να αντιστοιχίζει (αυθαίρετα) τον κάθε συνδυασμό των bits στο κάθε επιθυμητό στοιχείο. Με τον ίδιο αυτό τρόπο, οι δυαδικές λέξεις μπορούν να αναπαραστήσουν αριθμούς, αρκεί να επιλέξουμε τον επιθυμητό κώδικα. Γιά την αναπαράσταση των μη-αρνητικών ακεραίων (non-negative integers) (άλλως: "μη προσημασμένων ακεραίων" - unsigned integers) χρησιμοποιείται καθολικά η κωδικοποίηση του δυαδικού συστήματος μέτρησης που αποτελεί κατ' ευθείαν μεταφορά στη "βάση 2" των όσων ισχύουν στη "βάση 10", δηλαδή στο δεκαδικό σύστημα μέτρησης. Όπως ξέρουμε, ο δεκαδικός n-ψήφιος αριθμός "dn-1dn-2...d2d1d0", όπου τα "ψηφία" di (γιά i=0, 1, ..., n-1) είναι ακέραιοι αριθμοί μεταξύ του 0 και του 9, παριστάνει τον ακέραιο αριθμό: Dec Binary Oct Hex | Dec Binary Oct Hex | Dec Binary Oct Hex
00 000000 00 00 | 16 010000 20 10 | 32 100000 40 20
01 000001 01 01 | 17 010001 21 11 | 33 100001 41 21
02 000010 02 02 | 18 010010 22 12 | 34 100010 42 22
03 000011 03 03 | 19 010011 23 13 | ... ... ... ...
04 000100 04 04 | 20 010100 24 14 | 38 100110 46 26
05 000101 05 05 | 21 010101 25 15 | 39 100111 47 27
06 000110 06 06 | 22 010110 26 16 | 40 101000 50 28
07 000111 07 07 | 23 010111 27 17 | 41 101001 51 29
08 001000 10 08 | 24 011000 30 18 | 42 101010 52 2A
09 001001 11 09 | 25 011001 31 19 | ... ... ... ...
10 001010 12 0A | 26 011010 32 1A | 46 101110 56 2E
11 001011 13 0B | 27 011011 33 1B | 47 101111 57 2F
12 001100 14 0C | 28 011100 34 1C | 48 110000 60 30
13 001101 15 0D | 29 011101 35 1D | ... ... ... ...
14 001110 16 0E | 30 011110 36 1E | 62 111110 76 3E
15 001111 17 0F | 31 011111 37 1F | 63 111111 77 3F
| 64 1000000 100 40
Η μετατροπή αριθμού μεταξύ δυαδικού, οκταδικού, και δεκαεξαδικού είναι εντελώς τετριμένη, βάσει της εξής παρατήρησης: Επειδή η βάση H = 8 = 23, κάθε ψηφίο ενός οκταδικού αριθμού αντιστοιχεί ακριβώς σε μιά τριάδα από bits του ίδιου αριθμού γραμμένου στο δυαδικό, ξεκινώντας από δεξιά. Ομοίως, επειδή η βάση H = 16 = 24, κάθε ψηφίο ενός δεκαεξαδικού αριθμού αντιστοιχεί ακριβώς σε μιά τετράδα από bits του ίδιου αριθμού γραμμένου στο δυαδικό, ξεκινώντας πάλι από δεξιά.
Η μετατροπή αριθμού από το δυαδικό στο δεκαδικό μπορεί να γίνει όπως στο παράδειγμα στην αρχή της παραγράφου, προσθέτοντας δηλαδή τις δυνάμεις του 2 που αντιστοιχούν στους άσσους του αριθμού. Τέλος, η μετατροπή αριθμού από το δεκαδικό στο δυαδικό μπορεί να γίνει βάσει της παρατήρησης ότι αν ένας αριθμός είναι μονός (περιττός) τότε το λιγότερο σημαντικό (LS) bit του θα είναι άσσος, ενώ αν ο αριθμός είναι ζυγός (άρτιος) τότε το LS bit του θα είναι μηδέν. Πράγματι, αν ο αριθμός A είναι ο bn-1bn-2...b2b1b0, όπως παραπάνω, τότε διαιρώντας τον A διά 2 έχουμε:
Άσκηση 5.2: Μετατροπές Βάσης Αριθμών
[Άσκηση στο χαρτί· παράδοση μέσα στην αναφορά του εργαστηρίου].(α) Θεωρήστε δεκαεξάμπιτους (16-bit) μη προσημασμένους (unsigned) αριθμούς. Πόσα ψηφία θα έχουν αυτοί όταν εκφραστούν στο δεκαεξαδικό; Γιατί; Πόσα ψηφία στο οκταδικό; Γιατί; Στο οκταδικό, το αριστερότερό τους ψηφίο (περισσότερο σημαντικό - most significant - MS) τι μπορεί να είναι μόνο; Γιατί;
(β) Μετατρέψτε τους δεκαδικούς αριθμούς 9501 και 23848 σε δεκαεξάμπιτους δυαδικούς αριθμούς, δείχνοντας και τις ενδιάμεσες πράξεις που κάνετε. Στη συνέχεια, επαληθεύστε τις μετατροπές αυτές, βρίσκοντας από τους δυαδικούς αριθμούς τους δεκαδικούς στους οποίους αυτοί αντιστοιχούν. Τέλος, γράψτε τους δύο δεκαεξάμπιτους δυαδικούς αριθμούς που βρήκατε στο οκταδικό και στο δεκαεξαδικό, δείχνοντας καθαρά από που προκύπτει το κάθε ψηφίο του κάθε οκταδικού και δεκαεξαδικού αριθμού.
(γ) Θεωρήστε τον πενταψήφιο δεκαεξαδικό αριθμό 8FB7C. Πόσα bits έχει; Γιατί; Γράψτε τον στο δυαδικό και στη συνέχεια στο οκταδικό.
5.3 Πρόσθεση Δυαδικών Αριθμών: Αλγόριθμος "Κρατουμένου"
Έστω ότι θέλουμε να προσθέσουμε τους δυαδικούς αριθμούς, μεγέθους n bits ο καθένας, A = an-1an-2...a2a1a0 και B = bn-1bn-2...b2b1b0. Προφανώς, από μαθηματική άποψη, το άθροισμά τους είναι:Γιά να βρούμε το άθροισμα σε μορφή δυαδικής αναπαράστασης πρέπει να ακολουθήσουμε μιά διαδικασία ("αλγόριθμο"!) ανάλογη της πρόσθεση με "κρατούμενο" (carry) του δημοτικού σχολείου. Ξεκινάμε από τη λιγότερο σημαντική (LS) θέση (θέση 0), (a0+b0). Εάν το άθροισμα αυτό είναι 0 ή 1, τότε το ονομάζουμε s0, και αυτό αποτελεί το λιγότερο σημαντικό (LS) bit του αθροίσματος. Εάν όμως a0+b0 = 2, τότε εκφράζουμε το 2 στο δυαδικό (10), και επομένως θέτουμε s0 = 0 (αφού το άθροισμα είναι ζυγός αριθμός), και θυμόμαστε ότι μας έχει "περισσέψει" μιά ποσότητα 2·20 (όταν μας προέκυψε στη θέση 0) = 1·21 (όταν τη μεταφέρουμε στη θέση 1), την οποία και "κρατάμε" γιά να τη μεταφέρουμε στη θέση 1, ονομάζοντας την c1 (κρατούμενο - carry).
Συνεχίζοντας με τη θέση 1, πρέπει να προσθέσουμε τα bits a1 και b1 των δύο αριθμών, καθώς και το κρατούμενο c1 που προέκυψε από τη θέση 0. Καθένας από αυτούς τους τρείς αριθμούς είναι 0 ή 1 (το κρατούμενο μπορεί να ήταν "2" στη θέση 0, αλλά όταν μεταφέρθηκε στη θέση 1 έγινε το μισό ("1"), διότι η θέση 1 έχει διπλάσια "σημαντικότητα" (δύναμη του 2) από τη θέση 0). Αθροίζοντας αυτούς τους 3 αριθμούς, που καθένας τους είναι 0 ή 1, προκύπτει ένας αριθμός μεταξύ 0 και 3. Αν το άθροισμα αυτό είναι 0 ή 1, τότε το ονομάζουμε s1, και αυτό αποτελεί το bit του αθροίσματος στη θέση 1. Εάν όμως a1+b1+c1 είναι 2 ή 3, τότε το εκφράζουμε στο δυαδικό σαν έναν αριθμό των 2 bits (2 bits αρκούν!), ονομάζουμε s1 το δεξιό και c2 το αριστερό από αυτά τα 2 bits, και θυμόμαστε ότι μας έχει "περισσέψει" μιά ποσότητα 2c2·21 (όταν μας προέκυψε στη θέση 1) = c2·22 (όταν τη μεταφέρουμε στη θέση 2), την οποία και "κρατάμε" γιά να τη μεταφέρουμε στη θέση 2.
Από κει και πέρα, η διαδικασία (αλγόριθμος) της πρόσθεσης προχωρεί με τον ίδιο τρόπο. Η παρατήρηση-κλειδί ("αναλλοίωτη συνθήκη" - invariant property) είναι ότι το "κρατούμενο εισόδου" ci στη θέση i είναι πάντα 0 ή 1. Την ιδιότητα αυτή την αποδείξαμε στη θέση i=1, και την αποδεικνύουμε στη συνέχεια επαγωγικά, από τη θέση i γιά τη θέση i+1: αφού το άθροισμα (ai+bi+ci) είναι άθροισμα τριών αριθμών που καθένας τους είναι 0 ή 1, τότε το άθροισμα αυτό θα είναι μεταξύ 0 και 3, άρα μπορεί να εκφραστεί με μοναδικό τρόπο σαν δυαδικός αριθμός των 2 bits, ci+1·2i+1 + si·2i, όπου οι αριθμοί ci+1 και si είναι μεταξύ 0 και 1. Από αυτόν τον αλγόριθμο πρόσθεσης, λοιπόν, προέκυψαν τα n bits αθροίσματος si (i από 0 έως n-1) και το ένα τελικό bit κρατουμένου cn, τα οποία n+1 bits είναι όλα 0 ή 1, και γιά τα οποία ισχύει, από τον αλγόριθμο μετασχηματισμού της αρχικής μας σχέσης, ότι: A + B = cn·2n + sn-1·2n-1 + sn-2·2n-2 + ... + s2·22 + s1·21 + s0·20. Επειδή αυτή είναι μία νόμιμη αναπαράσταση του αθροίσματος A+B στο δυαδικό σύστημα, και επειδή η αναπαράσταση κάθε αριθμού στο δυαδικό σύστημα είναι μοναδική, προκύπτει ότι αυτή είναι η αναπαράσταση του αθροίσματος στο δυαδικό. Ο.Ε.Δ.
5.4 Ο Ψηφιακός Αθροιστής
Η διαδικασία πρόσθεσης που διατυπώσαμε παραπάνω μεταφράζεται άμεσα σε ψηφιακό κύκλωμα όπως φαίνεται στο σχήμα. Το παράδειγμα εδώ αφορά την πρόσθεση δύο οκτάμπιτων δυαδικών αριθμών, A και B. Κάθε ορθογώνιο κουτί παριστά ένα κύκλωμα πρόσθεσης γιά μία θέση σημαντικότητας των bits.
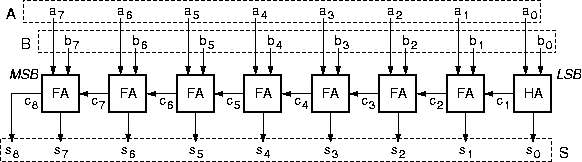
Το δεξιό (LS) κύκλωμα είναι απλούστερο από τα άλλα,
διότι έχει να προσθέσει μόνο δύο εισόδους (του ενός bit καθεμία)·
αυτό λέγεται "ημιαθροιστής" (half-adder, "HA").
Το άθροισμα που υπολογίζει το εκφράζει σαν δύο bits:
το bit s0 που έχει
τον ίδιο βαθμό σημαντικότητας με τις εισόδους (θέση 0),
και το bit c1 που έχει
βαθμό σημαντικότητας κατά 1 μεγαλύτερο αυτού των εισόδων.
Τα υπόλοιπα 7 κυκλώματα είναι κάπως πιό πολύπλοκα:
πρέπει να προσθέσουν τρείς εισόδους (του ενός bit) το καθένα·
αυτά λέγονται "πλήρεις αθροιστές" (full-adders, "FA").
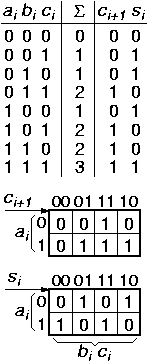 Ο ρόλος τους είναι να μετράνε
πόσοι άσσοι υπάρχουν στις τρείς εισόδους τους
και να εκφράζουν αυτό τον αριθμό στο δυαδικό, με 2 bits,
τα ci+1 και si.
Ο πίνακας αληθείας τους προκύπτει από αυτό τον ορισμό
και φαίνεται στο σχήμα δίπλα.
Παρατηρήστε ότι ο πίνακας αληθείας του αθροίσματος, s,
έχει τους άσσους σε σχήμα "σκακιέρας":
καμία απλοποίηση δεν είναι εφικτή!
Ο λόγος είναι ότι το s ισούται με
την "περιττή ισοτιμία" (odd parity) των εισόδων,
δηλαδή το αν το πλήθος των άσσων στις εισόδους
είναι περιττός (μονός) αριθμός.
Οιαδήποτε δύο γειτονικά τετράγωνα στο χάρτη Karnaugh
διαφέρουν μεταξύ τους κατά την τιμή
μίας και μόνο μίας μεταβλητής εισόδου·
άρα, αλλάζοντας τιμή αυτή η μία μόνο είσοδος
αλλάζει και η ισοτιμία της εισόδου
από άρτια σε περιττή ή από περιττή σε άρτια,
κι έτσι αλλάζει και το s.
Κατά βάθος, η περιττή ισοτιμία
είναι η επέκταση του αποκλειστικού-Ή
σε περισσότερες των δύο μεταβλητές εισόδου,
και η παραπάνω ιδιότητά του είναι αυτή ακριβώς που το κάνει χρήσιμο
σε διατάξεις όπως οι διακόπτες allez-retour
και οι κώδικες ανίχνευσης σφαλμάτων:
αν ένα οιοδήποτε bit εισόδου αλλάξει τιμή,
ο κώδικας αυτός αλλάζει επίσης τιμή
(§1.4)
Ο ρόλος τους είναι να μετράνε
πόσοι άσσοι υπάρχουν στις τρείς εισόδους τους
και να εκφράζουν αυτό τον αριθμό στο δυαδικό, με 2 bits,
τα ci+1 και si.
Ο πίνακας αληθείας τους προκύπτει από αυτό τον ορισμό
και φαίνεται στο σχήμα δίπλα.
Παρατηρήστε ότι ο πίνακας αληθείας του αθροίσματος, s,
έχει τους άσσους σε σχήμα "σκακιέρας":
καμία απλοποίηση δεν είναι εφικτή!
Ο λόγος είναι ότι το s ισούται με
την "περιττή ισοτιμία" (odd parity) των εισόδων,
δηλαδή το αν το πλήθος των άσσων στις εισόδους
είναι περιττός (μονός) αριθμός.
Οιαδήποτε δύο γειτονικά τετράγωνα στο χάρτη Karnaugh
διαφέρουν μεταξύ τους κατά την τιμή
μίας και μόνο μίας μεταβλητής εισόδου·
άρα, αλλάζοντας τιμή αυτή η μία μόνο είσοδος
αλλάζει και η ισοτιμία της εισόδου
από άρτια σε περιττή ή από περιττή σε άρτια,
κι έτσι αλλάζει και το s.
Κατά βάθος, η περιττή ισοτιμία
είναι η επέκταση του αποκλειστικού-Ή
σε περισσότερες των δύο μεταβλητές εισόδου,
και η παραπάνω ιδιότητά του είναι αυτή ακριβώς που το κάνει χρήσιμο
σε διατάξεις όπως οι διακόπτες allez-retour
και οι κώδικες ανίχνευσης σφαλμάτων:
αν ένα οιοδήποτε bit εισόδου αλλάξει τιμή,
ο κώδικας αυτός αλλάζει επίσης τιμή
(§1.4)
Το κρατούμενο εξόδου του κάθε αθροιστή είναι είσοδος στον επόμενο προς τα "αριστερά" (προς MS) αθροιστή. Στην αριστερότερη (MS) θέση, το κρατούμενο εξόδου πρέπει να θεωρηθεί ότι αποτελεί το επόμενο σε σημαντικότητα bit του αθροίσματος, αφού το άθροισμα δύο οκτάμπιτων αριθμών (από 0 έως 255 καθένας) ενδέχεται να απαιτεί 9 bits γιά να παρασταθεί (άθροισμα από 0 έως 510). Ο οκτάμπιτος αθροιστής που μόλις σχεδιάσαμε είναι ένα συνδυαστικό κύκλωμα, διότι οι έξοδοί του, S, εξαρτώνται μόνο από τις παρούσες τιμές των εισόδων του, A και B, δηλαδή δεν έχει μνήμη. Όταν συνθέταμε συνδυαστικά κυκλώματα είχαμε δεί τη μέθοδο του χάρτη Karnaugh, με την οποία το κύκλωμα εκφράζονταν σαν το λογικό Ή κάμποσων όρων που ο καθένας τους ήταν το λογικό ΚΑΙ εισόδων ή συμπληρωμάτων τους. Ακολουθόντας τη μέθοδο αυτή μπορεί κανείς να φτιάξει το ένα από τα κουτιά του σχήματος, όπως στη σελίδα 152 του βιβλίου. Όμως, αν προσπαθήσουμε να εφαρμόσουμε τη μέθοδο αυτή σε ολόκληρο τον (π.χ. οκτάμπιτο) αθροιστή, πρώτον ο χάρτης Karnaugh θα είναι τεραστίων διαστάσεων (216 τετράγωνα!), και δεύτερον το κύκλωμα που θα προέκυπτε θα ήταν εξωπραγματικά τεράστιο. Αντ' αυτού, το κύκλωμα που σχεδιάσαμε εδώ, στο παραπάνω σχήμα, είναι πολύ διαφορετικό: αποτελείται από πολλά υποκυκλώματα (ένα γιά κάθε θέση bit), όπου η έξοδος του ενός είναι είσοδος στο άλλο (κρατούμενα), δηλαδή πρόκειται γιά μιάν αλυσίδα πολλών κυκλωμάτων αντί γιά μόλις δύο επίπεδα πυλών (ΚΑΙ - Ή) που δίνει ο χάρτης Karnaugh. Το πλεονέκτημα της νέας μεθόδου είναι η τεράστια απλοποίηση του κυκλώματος. Το μειονέκτημα είναι η μεγαλύτερη καθυστέρηση: γιά να προκύψουν τα τελευταία 2 MS bits του αθροίσματος πρέπει πρώτα να τελειώσουν τη δουλειά τους, "σειριακά" ο ένας μετά τον άλλον, όλοι οι επιμέρους αθροιστές (ενός bit καθένας), από τη δεξιά μέχρι την αριστερή άκρη.
Άσκηση 5.5: Δυαδική Πρόσθεση
[Άσκηση στο χαρτί· παράδοση με την αναφορά του εργαστηρίου].Προσθέστε στο δυαδικό, με τον παραπάνω αλγόριθμο πρόσθεσης με κρατούμενα, τους δύο δεκαεξάμπιτους δυαδικούς αριθμούς που βρήκατε στην άσκηση 5.2(β) όταν μετατρέψατε τους δεκαδικούς αριθμούς 9501 και 23848 στο δυαδικό. Στη συνέχεια, μετατρέψτε το δυαδικό άθροισμα που βρήκατε στο δεκαδικό, και επαληθεύστε ότι αυτό ισούται με 9501+23848.
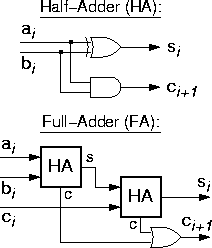
Άσκηση 5.6: Ημιαθροιστής (Half-Adder), Πλήρης Αθροιστής (Full-Adder)
Ονομάσαμε ημιαθροιστή (half-adder, HA) το κύκλωμα που προσθέτει δύο bits, ai και bi, και εκφράζει το άθροισμά τους σε μορφή ενός δυαδικού αριθμού 2 bits, ci+1si. Ονομάσαμε πλήρη αθροιστή (full-adder, FA) το κύκλωμα που προσθέτει τρία bits, ai, bi, και ci, και εκφράζει το άθροισμά τους σε μορφή ενός δυαδικού αριθμού 2 bits, ci+1si. Εκτός από την κατ'ευθείαν σύνθεσή του βάσει των χαρτών Karnaugh στο δεύτερο σχήμα της §5.4 παραπάνω (βλ. και σελ. 152 βιβλίου), το κύκλωμα αυτό μπορεί να κατασκευαστεί και χρησιμοποιώντας ημιαθροιστές όπως δείχνει το σχήμα εδώ: γιά να προσθέσω τρείς αριθμούς αρκεί να προσθέσω τους δύο πρώτους και στο άθροισμά τους να προσθέσω τον τρίτο. Κανονικά, πρέπει επίσης να προσθέσω και τα κρατούμενα. Όμως, μπορεί κανείς εύκολα να αποδείξει ότι το πολύ ένας από τους δύο ημιαθροιστές του σχήματος μπορεί να βγάζει κρατούμενο 1, κάθε φορά· άρα, αντί γιά κύκλωμα πρόσθεσης των δύο επιμέρους κρατουμένων, αρκεί να χρησιμοποιηθεί μιά πύλη Ή. Γιά την άσκηση αυτή:- Κατασκευάστε τον πίνακα αληθείας του ημιαθροιστή, και αποδείξτε μ' αυτόν ότι ο ημιαθροιστής μπορεί να υλοποιηθεί όπως δείχνει το σχήμα. Η επάνω πύλη στο σχήμα, της οποίας το σύμβολο μοιάζει με πύλη Ή αλλά έχει διπλό τόξο στην αριστερή της πλευρά, είναι πύλη αποκλειστικού Ή (§1.4).
- Γράψτε την απόδειξη της παραπάνω ιδιότητας σχετικά με τα κρατούμενα εξόδου των δύο ημιαθροιστών του πλήρους αθροιστή.
- Κατασκευάστε τον πίνακα αληθείας του κυκλώματος με τους δύο ημιαθροιστές και την πύλη Ή που φαίνεται στο σχήμα, και συγκρίνετέ τον με τον πίνακα αληθείας του πλήρη αθροιστή που φαίνονταν στο δεύτερο σχήμα της §5.4 παραπάνω, αποδεικνύοντας έτσι ότι το κύκλωμα του σχήματος υλοποιεί όντως έναν πλήρη αθροιστή.
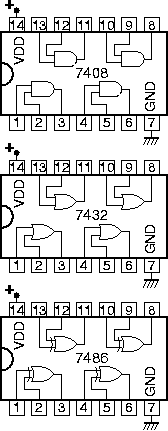
Πείραμα 5.7: Κατασκευή Ημιαθροιστή και Πλήρη Αθροιστή
Κατασκευάστε και ελέγξτε έναν ημιαθροιστή, και στη συνέχεια προσθέστε άλλον έναν ημιαθροιστή και την πύλη Ή όπως στο παραπάνω κύκλωμα της §5.6 προκειμένου να φτιάξτε και να ελέγξτε έναν πλήρη αθροιστή. Χρησιμοποιήστε, από τα chips που σας έχουν δοθεί (§3.6) ένα chip 7408 (πύλες AND), ένα chip 7432 (πύλες OR), και ένα chip 7486 που περιέχει 4 πύλες Αποκλειστικού-Ή (XOR). Οι ακροδέκτες των chips αυτών φαίνονται στο σχήμα. Πρίν φτάσετε στο εργαστήριο δείξτε τις συνδέσεις που πρέπει να γίνουν σ' αυτά τα chips προκειμένου να υλοποιήστε έναν ημιαθροιστή, και στη συνέχεια ένα πλήρη αθροιστή. Ακολουθήστε το μοντέλο του σχήματος της §4.10 γιά το σχεδιάγραμμα του κυκλώματός σας. Στο εργαστήριο, κατασκευάστε τα κυκλώματα αυτά, αφήνοντας χώρο στην πλακέτα συνδέσεων γιά ακόμα ένα chip 7408 και ένα chip 7486, καθώς και ένα ακόμα chip προς την πλευρά των εξόδων γιά το πείραμα 5.8. Θυμηθείτε τις οδηγίες κατασκευής και αποσφαλμάτωσης της §4.11. Ελέγξτε τη σωστή λειτουργία, πρώτα του ημιαθροιστή και μετά του πλήρη αθροιστή, τροφοδοτώντας τις εισόδους τους από τους διακόπτες Q, M, N, και παρακολουθώντας τις εξόδους τους στις LED 0 και 1. Όταν τελειώσετε μην χαλάσετε το κύκλωμά σας, διότι θα το χρειαστείτε στο πείραμα 5.11.Πείραμα 5.8: Chip Αποκωδικοποίησης Οθόνης 7 Τμημάτων
Τα κυκλώματα αποκωδικοποίησης τεσσάρων bits γιά να οδηγήσουν τον ενδείκτη 7 τμημάτων που είδαμε στην άσκηση 4.5 ήταν πολύ πολύπλοκα γιά να τα φτιάξουμε στην πλακέτα μας, ξεκινόντας με απλές πύλες AND, OR, και NOT. Γι' αυτό θα τα πάρουμε έτοιμα! Το chip MC14511B κάνει περίπου τη δουλειά του κυκλώματος της άσκησης 4.5 συν μερικές ακόμα. Πρόκειται γιά έναν αποκωδικοποιητή από "BCD" (binary-coded decimal - δεκαδικό σε δυαδική κωδικοποίηση) σε οθόνη 7 τμημάτων (§2.1). Ο κώδικας BCD αποτελείται από 4 bits τα οποία παίρνουν μόνο τις τιμές από 0000 έως 1001 που είδαμε στην άσκηση 4.4. Το chip MC14511B έχει 7 εξόδους, οι οποίες οδηγούν κατ' ευθείαν τις LED's a, b, c, d, e, f και g της οθόνης 7 τμημάτων, με τον τρόπο που έδειχνε η άσκηση 4.5 (μόνο που το "7" δεν έχει αριστερή κατακόρυφη γραμμή). Επιπλέον, το chip MC14511B σβήνει εντελώς την οθόνη όταν στην είσοδό του δοθεί ένας από τους υπόλοιπους 6 κώδικες, από 1010 έως 1111 (δηλαδή δεν έχει "συνθήκες αδιαφορίας" - §4.4).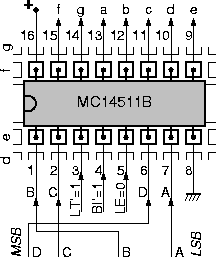 Μερικές ακόμα δυνατότητές του θα αναφερθούν παρακάτω,
αλλά δεν θα τις χρησιμοποιήσουμε εμείς.
Λεπτομερείς πληροφορίες γιά το chip αυτό μπορείτε να βρείτε
στη διεύθυνση που ανέφερε η
§3.6
ή π.χ. στη διεύθυνση
http://www.onsemi.com/pub/Collateral/MC14511B-D.PDF
Μερικές ακόμα δυνατότητές του θα αναφερθούν παρακάτω,
αλλά δεν θα τις χρησιμοποιήσουμε εμείς.
Λεπτομερείς πληροφορίες γιά το chip αυτό μπορείτε να βρείτε
στη διεύθυνση που ανέφερε η
§3.6
ή π.χ. στη διεύθυνση
http://www.onsemi.com/pub/Collateral/MC14511B-D.PDF
Οι ακροδέκτες του chip MC14511B φαίνονται στο σχήμα. Η ηλεκτρική τροφοδοσία του chip γίνεται από το κάτω δεξιά ποδαράκι (αριθμός 8) γιά τον αρνητικό πόλο (γείωση) και από το πάνω αριστερό (αριθμός 16) γιά το θετικό πόλο. Τα ποδαράκια 9 έως και 15 του MC14511B είναι οι 7 έξοδοί του, που προορίζονται να οδηγούν κατ' ευθείαν τις 7 LED's· συνδέστε τα στις επαφές a, b, c, d, e, f και g της καλωδιοταινίας, προσέχοντας τη διαφορετική σειρά. Το ποδαράκι 3 είναι είσοδος, και είναι το αρνητικό (συμπλήρωμα) του σήματος LT - lamp test, που προορίζεται γιά τον έλεγχο μήπως κάποια λυχνία έχει καεί: όταν ενεργοποιείται πρέπει να ανάβουν όλες οι λυχνίες --όποια δεν ανάβει έχει καεί. Εμείς δεν θα το χρησιμοποιήσουμε, δηλαδή LT=0, δηλαδή LT'=1, άρα πρέπει να τροφοδοτήσετε το ποδαράκι 3 με ψηλή τάση, δηλαδή να το συνδέσετε στο θετικό πόλο του τροφοδοτικού. Το ποδαράκι 4 είναι είσοδος, και είναι το αρνητικό του σήματος BI - blanking input, που προορίζεται γιά να σβήνει την οθόνη όποτε θέλουμε να τη σβήνουμε (ανεξαρτήτως κώδικα εισόδου)· εμείς δεν θα το χρησιμοποιήσουμε, δηλαδή BI=0, δηλαδή BI'=1, άρα και το ποδαράκι 4 πρέπει να το συνδέσετε στη θετική τροφοδοσία. Το ποδαράκι 5 είναι η είσοδος LE - latch enable, που προορίζεται γιά να αποθηκεύεται ο κώδικας εισόδου σε 4 εσωτερικά flip-flops, ούτως ώστε να παραμένει η οθόνη στεθερή στην ένδειξη που είχε επιλεγεί παλαιότερα μέσω των εισόδων, ανεξάρτητα αν οι είσοδοι αυτές τώρα έχουν αλλάξει· εμείς δεν θα το χρησιμοποιήσουμε, δηλαδή LE=0, άρα και το ποδαράκι 5 πρέπει να το συνδέσετε στην αρνητική τροφοδοσία, δηλαδή στη γείωση.
Τέλος, τα ποδαράκια 1, 2, 6, και 7 είναι οι είσοδοι του κώδικα BCD που δίνουμε γιά να ελέγχουμε τον αριθμό στην οθόνη. Το MC14511B χρησιμοποιεί το συμβολισμό DCBA γιά τα 4 αυτά bits, δηλαδή "D" (ποδαράκι 6) είναι το περισσότερο σημαντικό (MS) bit, και "A" (ποδαράκι 7) είναι το λιγότερο σημαντικό (LS) bit. Τροφοδοτήστε αυτούς τους 4 ακροδέκτες από τους διακόπτες Q (MS bit), M, N, και A (LS bit), και ελέξγτε τι αποτέλεσμα φέρνουν οι 16 συνδυασμοί των 4 αυτών εισόδων στην ένδειξη 7 τμημάτων.
Άσκηση 5.9: Ταχύτητα Δυαδικής Πρόσθεσης
[Άσκηση στο χαρτί· παράδοση μέσα στην αναφορά του εργαστηρίου].Θεωρήστε ότι η κάθε λογική πύλη έχει καθυστέρηση 75 ps, δηλαδή η έξοδός της παίρνει τη σωστή καινούργια τιμή 75 ps μετά την αλλαγή μιάς εισόδου σε μιά νέα "σωστή" τιμή. Στην πράξη, η καθυστέρηση μιάς πύλης κυμαίνεται σε μιά ευρεία περιοχή τιμών, εξαρτώμενη από πολλούς παράγοντες· πάντως, η τιμή που υποθέτουμε --λιγότερο από ένα δέκατο του δισεκατομμυριοστού του δευτερολέπτου-- είναι αντιπροσωπευτική του τι συμβαίνει μέσα σ' ένα σύγχρονο (2004) επεξεργαστή με ρολόϊ 1 GHz ή λίγο παραπάνω. Προσοχή: η τιμή που υποθέτουμε είναι πολύ μικρότερη από την καθυστέρηση των πυλών των chips 7408, 7432, και 7486, πρώτ' απ' όλα επειδή εκείνες οι καθυστερήσεις αφορούν σήματα που είναι έξω από το chip, ενώ εδώ μιλάμε γιά σήματα μέσα στο ίδιο chip, και δεύτερον επειδή εδώ υποθέτουμε πιό σύγχρονη τεχνολογία κατασκευής. Υπενθύμιση: τα υποπολλαπλάσια της μονάδας είναι:
- m - milli - χιλιοστό - 10-3
- μ - micro - εκατομμυριοστό - 10-6
- n - nano - δισεκατομμυριοστό - 10-9
- p - pico - τρισεκατομμυριοστό - 10-12
- f - femto - τετράκις εκατομμυριοστό - 10-15
- a - atto - πεντάκις εκατομμυριοστό - 10-18
(β) Θεωρήστε έναν αθροιστή λέξεων των 64 bits, όπως αυτοί που υπάρχουν στους σύγχρονους 64-μπιτους επεξεργαστές. Τι καθυστέρηση θα είχε ένας τέτοιος αθροιστής αν ήταν κατασκευασμένος από μιάν αλυσίδα 64 πλήρων αθροιστών σαν αυτούς του (α), όπως έδειχνε το σχήμα της σελίδας 3; Γιά απλότητα, θεωρήστε ότι ο ημιαθροιστής του δεξιού bit έχει κι αυτός την ίδια καθυστέρηση.
(γ) Αν η περίοδος του ρολογιού του επεξεργαστή ήταν περίπου ίση με την καθυστέρηση του αθροιστή (όπως συχνά είναι), τι συχνότητα ρολογιού θα είχε αυτός ο επεξεργαστής; Πώς συγκρίνεται αυτή με τις συχνότητες ρολογιών των σύγχρονων επεξεργαστών; [Ευτυχώς, υπάρχουν τρόποι να γίνονται πολύ γρηγορότερα οι προσθέσεις, γι' αυτό και οι επεξεργαστές είναι τόσο γρήγοροι όσο είναι!...]
 5.10 Πρόσθεση πολλών Αριθμών
5.10 Πρόσθεση πολλών Αριθμών
Όταν θέλουμε να βρούμε το άθροισμα πολλών αριθμών,
μπορούμε είτε να χρησιμοποιήσουμε έναν αθροιστή κατ' επανάληψη,
όπως θα δούμε αργότερα,
όταν θα μιλάμε γιά "ακολουθιακά" --δηλ. όχι συνδυαστικά-- κυκλώματα,
ή να χρησιμοποιήσουμε πολλούς αθροιστές,
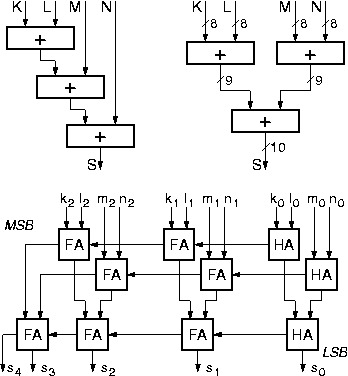
όπως δείχνει το σχήμα.
Στο παράδειγμα του σχήματος εδώ,
ζητάμε το άθροισμα S των τεσσάρων αριθμών K, L, M, και N,
άρα πρέπει να κάνουμε τρείς προσθέσεις.
Με την πάνω αριστερά διάταξη (σε σχήμα καταρράκτη - cascade),
ο πρώτος αθροιστής προσθέτει τους K και L,
ο δεύτερος προσθέτει το άθροισμα K+L με τον M,
και ο τρίτος βρίσκει το άθροισμα του K+L+M με τον N.
Με την πάνω δεξιά διάταξη (σε σχήμα δένδρου - tree),
βρίσκουμε πρώτα τα αθροίσματα K+L και M+N,
και στη συνέχεια τα προσθέτουμε.
Εάν θεωρήσουμε, π.χ., ότι οι αριθμοί K, L, M, N είναι οκτάμπιτοι,
δηλαδή μεταξύ 0 και 255 καθένας,
τότε το άθροισμά τους μπορεί να κυμαίνεται από 0 έως 1020,
άρα χρειάζονται 10 bits γιά να παρασταθεί.
Παρ' ότι και οι δύο διατάξεις χρησιμοποιούν το ίδιο πλήθος αθροιστών,
η δενδροειδής είναι γενικά προτιμότερη,
διότι συνήθως δίνει μικρότερη συνολική καθυστέρηση
(αν και, όπως δείχνει το κάτω μέρος του σχήματος,
η συνολική καθυστέρηση,
όταν χρησιμοποιήσουμε αθροιστές του τύπου της παραγράφου 5.4,
δεν είναι τόσο άσχημη όσο δείχνει το πάνω μέρος του σχήματος).
Στο κάτω μέρος του σχήματος φαίνεται η δενδροειδής διάταξη των τριών αθροιστών, όπου έχουμε αναλύσει τον κάθε αθροιστή σε κυκλώματα του ενός bit, όπως κάναμε παραπάνω στην παράγραφο 5.4· γιά να χωράει το σχήμα, περιοριστήκαμε σε τρίμπιτους αριθμούς, αντί 8 bits που είχαν στο επάνω μέρος του σχήματος. Προσέξτε ότι όλα τα bits της ίδιας "σημαντικότητας" (δηλαδή που είναι συντελεστές της ίδιας δύναμης του 2) --π.χ. τα k1, l1, m1, n1-- προστίθενται μεταξύ τους με πλήρεις αθροιστές (FA) αυτής της "σημαντικότητας", δηλαδή τα ενδιάμεσα αθροίσματα που παράγουν αυτά τα κυκλώματα FA έχουν την ίδια αυτή σημαντικότητα 1, και προστίθενται μεταξύ τους (ή θα μπορούσαν να προστεθούν και με τα bits ίδιας σημαντικότητας άλλων αριθμών, π.χ. p1) γιά να παράγουν το bit s1 του αθροίσματος που έχει κι αυτό την ίδια σημαντικότητα 1. Όμως, τα κρατούμενα εξόδου όλων αυτών των κυκλωμάτων FA έχουν σημαντικότητα κατά ένα μεγαλύτερη, διότι αποτελούν συντελεστές της επόμενης προς τα αριστερά δύναμης του 2, άρα πρέπει να αθροιστούν με τα bits εισόδου της αντίστοιχης σημαντικότητας 2, εδώ, δηλαδή με τα k2, l2, m2, και n2. Οι προσθέσεις αυτών των 7 bits σημαντικότητας 2 (4 bits εισόδου και 3 κρατούμενα) πρέπει να γίνουν σε κυκλώματα FA (ή HA) σημαντικότητας 2, με οιαδήποτε σειρά ή σε οιοδήποτε μίγμα προτιμάμε.
Πείραμα 5.11: Μετρητής Πλήθους πατημένων Διακοπτών
Σχεδιάστε και κατασκευάστε ένα κύκλωμα με έξι (6) εισόδους που να μετράει πόσες από αυτές ισούνται με 1, και να δείχνει το πλήθος αυτό, σαν δεκαδικό αριθμό, στην οθόνη 7 τμημάτων. Μας ενδιαφέρει μόνο το πλήθος των "αναμένων" εισόδων και όχι το ποιές από αυτές είναι αναμένες (ισούνται με 1). Άρα, το αποτέλεσμα θα είναι ένας αριθμός από 0 έως 6, τον οποίο το κύκλωμά σας πρέπει κατ' αρχάς να υπολογίσει σαν τρίμπιτο δυαδικό αριθμό, μεταξύ 000 και 110· στη συνέχεια, με τον αριθμό αυτό θα οδηγήστε τον αποκωδικοποιητή BCD σε ενδείκτη 7 τμημάτων του πειράματος 5.8 παραπάνω. Εάν όταν φτάσετε σε αυτό το πείραμα, στο εργαστήριο, είναι η ώρα περασμένη και κινδυνεύετε να μην προλάβετε να κατασκευάσετε το πλήρες κύκλωμα με τις 6 εισόδους, ξεκινήστε με ένα υποσύνολό του που να μετράει τους άσσους μεταξύ τεσσάρων (4) μόνο εισόδων, και στη συνέχεια, αν αυτό δουλεύει σωστά και έχετε χρόνο, συμπληρώστε το σε 6 εισόδους.Ακολουθήστε την εξής στρατηγική: θεωρήστε ότι κάθε είσοδος είναι ένας (μονόμπιτος!) δυαδικός αριθμός· άρα, πρέπει να προσθέσετε έξι (6) δυαδικούς αριθμούς του 1 bit καθένας, και να βγάλετε ένα άθροισμα των 3 bits (το οποίο ποτέ δεν θα υπερβαίνει το 110). Μπορείτε να χρησιμοποιήστε το κύκλωμα της προηγουμένης παραγράφου 5.10 κατάλληλα προσαρμοσμένο. Στη βαθμίδα σημαντικότητας 0 του κυκλώματος, μπορείτε να προσθέσετε τους έξι αριθμούς είτε ανά δύο μέσω τριών ημιαθροιστών, είτε ανά τρείς μέσω δύο πλήρων αθροιστών· στη συνέχεια, τα τρία ή δύο αθροίσματα σημαντικότητας 0 πρέπει να προστεθούν μεταξύ τους, κατάλληλα. Τα κρατούμενα εξόδου από τους αθροιστές σημαντικότητας 0 θα αποτελούν εισόδους στη βαθμίδα σημαντικότητας 1. Πόσα είναι αυτά; Με τι κύκλωμα θα τα προσθέσετε; Μήπως ισχύει κάποια ιδιότητα όπως π.χ. ότι αποκλείεται να είναι ποτέ όλα τους ταυτόχρονα 1; Βάσει αυτής της ιδιότητας προκύπτει κάποια απλοποίηση του κυκλώματος; Ποιό από όλα τα κυκλώματα είναι φτηνότερο στην κατασκευή; Εξετάστε τις εναλλακτικές λύσεις πρίν φτάστε στο εργαστήριο, γράψτε τα συμπεράσματά σας στην αναφορά σας, καταλήξτε σε μία λύση και σχεδιάστε την, πρώτα με ημιαθροιστές ή/και πλήρεις αθροιστές και πύλες, μετά μόνο με ημιαθροιστές και πύλες, και στη συνέχεια με σκέτες πύλες. Στο τελευταίο στάδιο, ακολουθήστε το μοντέλο του σχήματος της §4.10 γιά το σχεδιάγραμμα του κυκλώματός σας.
Στο εργαστήριο, κατασκευάστε το κύκλωμά σας και τροφοδοτήστε το από τους διακόπτες Q, M, N, A, B, και C. Συνδέστε τη δυαδική έξοδο (3 bits) του κυκλώματος πρόσθεσης π.χ. στις LED 5, 6, και 7, και αν θέλετε συνδέστε και άλλες ενδιάμεσες εξόδους σε άλλες LED γιά σκοπούς παρακολούθησης - αποσφαλμάτωσης (βλ. και οδηγίες §4.11). Επίσης, συνδέστε τη δυαδική έξοδο (3 bits) του κυκλώματος πρόσθεσης στις τρείς LS εισόδους "CBA" του αποκωδικοποιητή του πειράματος 5.8, και τροφοδοτήστε την είσοδο D (4ο, MS bit) με 0 (δηλαδή συνδέστε την στη γείωση). Ελέξτε αν η ένδειξη 7 τμημάτων δείχνει πάντα το σωστό πλήθος πατημένων διακοπτών, γιά όλους τους συνδυασμούς κατάστασης των διακοπτών (64 συνδυασμοί!).
Εν συνεχεία, συνδέστε τη δυαδική έξοδο (3 bits) του κυκλώματος πρόσθεσης στις εισόδους DCB (3 MS bits) αυτή τη φορά, και τροφοδοτήστε την είσοδο A με 0. Αυτή η "ολίσθηση" προς τα αριστερά του πλήθους αναμένων εισόδων ισοδυναμεί με πολλαπλασιασμό επί 2. Ελέξτε αν η ένδειξη 7 τμημάτων ισούται πάντα με το διπλάσιο του πλήθους αναμένων εισόδων, εκτός όταν το πλήθος αυτό είναι 5 ή 6, οπότε το διπλάσιό τους δεν παριστάνεται με ένα μόνο δεκαδικό ψηφίο.
Μετά, αλλάξτε την είσοδο A σε 1 (σύνδεση στη θετική τροφοδοσία).
Ελέξτε αν η ένδειξη 7 τμημάτων
ισούται πάντα με το διπλάσιο συν ένα του πλήθους αναμένων εισόδων
(εκτός όταν ο αριθμός αυτός υπερβαίνει το 9)·
γιατί ισχύει αυτό;
|
[Up - Table of Contents] [Prev - 4. Karnaugh, RAM] |
[printer version - PDF] [6. Signed Int., Subtr. - Next] |
| Up to the Home Page of CS-120
|
© copyright
University of Crete, Greece.
last updated: 29 Oct. 2007, by M. Katevenis. |