Deriving Specifications for Composite Web Services

 
George Baryannis Manuel Carro Dimitris Plexousakis
Department of Computer Science School of Computer Science Department of Computer Science
University of Crete Universidad Politécnica de Madrid (UPM) and University of Crete
GR 71409 Heraklion, Greece IMDEA Software Institute, Madrid, Spain GR 71409 Heraklion, Greece
Email: gmparg@csd.uoc.gr Email: manuel.carro@imdea.org Email: dp@csd.uoc.gr

 

Abstract

We address the problem of synthesizing specifications for composite Web services, starting from those of their component services. Unlike related work in programming languages, we assume the definition of the component services (i.e. their code) to be unavailable - at best, they are known by a specification which (safely) approximates their functional behavior. Within this scenario, we deduce general formula schemes to derive specifications for basic constructs such as sequential, parallel compositions and conditionals and provide details on how to handle the special cases of loops and asynchronous execution. The resulting specifications facilitate service verification and service evolution as well as auditing processes, promoting trust between the involved partners.

Keywords

specification of service compositions, inference of specifications, service composition

I.  Introduction

Service composition enables service-based systems to be built using accepted engineering principles, such as (service) reusability and composability. Composite services provide value-added services that achieve functionality otherwise unattainable by atomic services. In order to fully achieve these goals, composite services should be made available to consumers in the same way as atomic services are, abstracting away complex details of the way participating services are orchestrated to achieve the required functionality. This allows service consumers to invoke services regardless of the way they are implemented (i.e. as an atomic service or as a composition of services). This can be accomplished by providing formal specifications of composite services which present to the end user the minimum information required to understand the functionality offered, often by describing the inputs, outputs, preconditions and effects (collectively known as IOPEs) of the composite service.
Formal specifications are indispensable in a variety of service-related activities. Similarly to the case of programming specifications, service specifications could be used as a basis to construct a service based on a set of requirements agreed upon by the parties involved, or to check that some existing specification meets a set of requirements. Furthermore, they can assist in auditing processes that check third party or legacy code conformance to specifications, promoting trust between digital society partners, since specification conformance is one step towards trustworthiness.
Specifications also play a major role in verification techniques. Verification involves checking whether a system (such as a service or a service composition) satisfies a property given the particular property and a formal description (i.e. a specification) of the system. Moreover, specifications are important when evaluating the results of service adaptation or service evolution [1]. For instance, it is fundamental to ensure that a new version of a composite service adheres to either the original specification or an evolved specification that has the same or fewer requirements (equal or weaker preconditions) and produces the same or more results (equal or stronger postconditions).
Composite specifications also offer great assistance when one attempts to deduce whether a set of services can actually be composed in a meaningful way. During the process of creating the composite specifications, inconsistencies may be detected between preconditions and/or postconditions of the participating services, rendering that particular set of services not composable. Thus, such problems can be prevented before the composite service is delivered to the end user, so that they may be resolved by replacing the service or services that cause the inconsistencies.
While existing service description frameworks attempt to describe service compositions using a variety of composition models ranging from orchestrations to choreographies to Finite State Machines, no attempt (to the best of our knowledge) has been made to handle the problem of automatically producing specifications for a composite service, based on the specifications of the participating services. The same is true for automated Web service composition approaches: while each of them offers a way of automatically or semi-automatically producing the composition schema, as well as the control and data flows of the composite services, none attempts to derive a complete specification of the service that is to be delivered to the service consumer.
Traditional tasks involving specifications, especially in the field of programming languages, include generating code out of specifications, using specification languages such as VDM [2], Z [3], B [4] or Event-B [5], generating specifications from existing code (i.e. the weakest precondition calculus [6]) or checking that a particular code conforms to a specification. The case handled in this paper is different: we aim at inferring specifications for a set of individual components, functioning as a whole, which are only known through their specifications. Therefore we cannot rely on the implementation in order to ensure that the service behavior agrees with the specification or use the implementation to deduce preconditions based on some predicate transformer. The only available knowledge is the specifications of the participating services and the composition schema. Our approach involves characterizing the meaning of the particular control structure used in the composition by means of the existing preconditions and postconditions, followed by a definition of a composite specification which is syntactically similar to the atomic specifications, in order to be able to recursively reason with it in a homogeneous way.
The rest of this paper is organized as follows. Section II offers a motivating example that illustrates the issues behind creating a composite specification. Section III provides an analytical description of the derivation process for most fundamental control constructs. Section IV deals with the cases of loops and asynchronous interaction. Section V offers a brief description of work related to specification derivation and Section VI concludes and points out topics for future work.

II.  Motivation

In this section, we present a rather indicative motivating example that attempts to illustrate the need for service composition specification in a service evolution scenario, as well as the issues behind deriving a composite specification, given the specifications of the participating services. The example is based on the E-Government case study of the European Network of Excellence S-Cube [7].
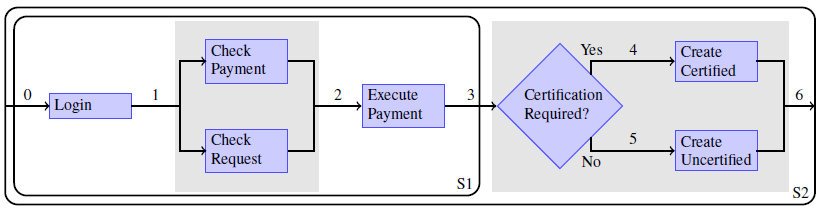
Composite process of the motivating example
Figure 1: Composite process of the motivating example
In this case study, citizens submit applications to request some government-related service, such as obtaining government-issued documents. A fee is required to obtain a particular document, so a mechanism that executes payment transactions is involved. Moreover, the citizen may request that the resulting document be authenticated. To that end, a digital signature certification mechanism is provided. A typical process to obtain a document is illustrated in Figure 1. Users log into the system and fill in forms regarding their request as well as payment details, which are then simultaneously processed before the payment process can begin. If users demand authentication for their documents, then a certification process is executed, resulting in the delivery of a certified document to the user. Otherwise, an uncertified document is delivered. For reasons that will be clarified in the sequel, we have labeled the states before and after particular points in the process. For instance, state 1 is the state after the completion of Login and before beginning execution of services CheckRequest and CheckPayment, while state 2 is the state following CheckRequest/CheckPayment and before invoking the ExecutePayment service.
Let us assume that the individual tasks described above are implemented as Web services. Table I offers a possible specification of the services involved in the process, in terms of their preconditions and postconditions, expressed in first-order logic. si and so denote the states before and after execution of the particular service respectively. Suppose that, at first, we have a composite service S1 that is implemented according to a specification T1 in order to handle the document purchase process we described, but without certification, as shown in Figure 1. Then, it is decided that some documents should be certified with a digital signature, so the initial specification is augmented to T2 to take that into consideration. In order to meet the new requirements, service S1 needs to be evolved into a new composite service S2. We need to check if the evolved service S2 meets the new specification T2. What we can do is derive a composite specification I(S2) based only on the information at hand (the orchestration definition of S2 and the specifications of the participating services) and check if I(S2) subsumes T2.

Service PreconditionsPostconditions
Login Valid(user,si) ∧¬LoggedIn(user,si)LoggedIn(user,so)
CheckRequest FilledIn(request,si) ∧LoggedIn(user,si)Valid(request,so)
CheckPayment FilledIn(payForm,si) ∧LoggedIn(user,si)Valid(payForm,so)
ExecutePayment Valid(payForm,si)PayCompleted(doc, user,so)
CreateCertified PayCompleted(doc, user,si) CertifCompleted(doc, user,so) ∧ Delivered(certifDoc,so)
CreateUncertified PayCompleted(doc, user,si)Delivered(doc,so)
Table 1: Atomic Service Specifications
The composite specification should explicitly state all conditions that must be true before the execution of the whole composite service, as well as all conditions that are true after a successful execution. While we have preconditions and postconditions for each participating service, there is no obvious way of deciding which part of them will be included in the composite specification. The resulting specification should be based on the way the services are orchestrated, taking into account the control and data flow of the composition.
We propose a derivation process that is based on structural induction and attempts to construct the composite specification using a bottom-up approach. The approach is applicable on any block-structured process, as well as graph-based ones, provided they can be transformed to block-structured equivalents [8]. The approach is based on the availability of the composition schema, which can be obtained, for instance, from the BPEL document of the composite service. In our example, the composite process is actually a sequence of services, which are either atomic (the Login and ExecutePayment services) or composite themselves (an AND-Split/AND-Join and an If-Then-Else execution). We need to first derive the specifications for the two inner compositions and then move a step up and derive the final composite specification, given the specifications for all four services of the sequence. In order to achieve this, we need to formulate the derivation for all fundamental control constructs, which we handle in the following section.

III.  Calculating Pre- and Post-Conditions

Formal specifications have been extensively used in computer science in order to rigorously describe what a system should do and can also similarly be used to offer a formal presentation of what a Web service provides and under which circumstances. A traditional format for a specification contains the conditions that should be met prior to execution (called preconditions, which we will denote by P) and the conditions that result after a successful execution of the program (called postconditions or results, denoted by Q).
In contrast to program specifications where preconditions are usually the weakest possible ones (and postconditions the strongest possible), in the case of services, P and Q can be expected to be safe approximations, e.g., P can be stronger than the weakest possible precondition for that particular service. P can therefore disallow invocations in cases where the actual code would work, but it would not allow invocations in a state not entailed by the weakest precondition. Note that if the approximation were done in the opposite direction, i.e., with P being weaker than the weakest precondition, executions allowed by P could be erroneous.

A.  Specification Semantics

A FOL semantics for a service specification with regard to its preconditions and postconditions is:
∀x ·(P(x,si) ⇒ ∃y ·Q(x, y,so))
P(x, si) and Q(x, y, so) are the (approximations of) preconditions and postconditions, respectively, using predicates, where x and y are vector variables that represent accordingly the input fed to the service and the returned output. si and so are fixed for a given composition schema and denote execution points. The reason for using such state identifiers as additional arguments to the predicates is to differentiate the truth value of predicates based on when they are evaluated, without having to carry around a usually cumbersome notion of state of the world. This allows us to express fluency in predicate values in a lean way. Other formalisms could be employed, such as the situation calculus (and variants, such as the fluent calculus), that are specifically designed for the description of dynamic domains. However, it should be noted that situation calculus can be encoded as a logic program [9,10], which has equivalent expressive power to FOL. Therefore by choosing FOL, we are not losing any power, while at the same time staying in a widely known formalism. Moreover, while the logical consequence in FOL may be semi-decidable, automated theorem provers for FOL, such as Prover9 [11] which is employed for the proofs in this work, are mature enough to provide high performance in practice.
Given similar specifications for the services participating in a composition, we want to construct a specification for the composite service c, which essentially involves calculating a set Pc of preconditions and a set Qc of postconditions such that the following holds:

∀x ·(Pc(x,si) ⇒ ∃y ·Qc(x, y,so))
where Pc(x,si) and Qc(x,y,so) are built using the preconditions and postconditions of the component services.
We insist that the derived specifications maintain the approximation that we mentioned earlier: preconditions for c derived from preconditions that are not the weakest themselves should be stronger than (or at least as strong as) the weakest possible precondition for the composition. We will return to this issue in Section V. In the following subsections, we will show how to calculate preconditions and postconditions for the most fundamental control constructs: sequences, AND-Split/AND-Join, OR-Split/OR-Join, XOR-Split/XOR-Join and conditionals [12,13]. In all cases, we consider compositions of two services, but it is straightforward to extend our work to more complex cases.

B.  Sequence

We denote sequential invocation by A(x, z);B(z, y), where all variables z that constitute the input of service B are produced as an output of service A. This includes variables which are input for B and which do not result from the execution of A, but come directly from sources external to the sequence. For the purposes of the specification we consider them to be routed untouched through A. a, b, and c respectively denote the state before the execution of A, after the execution of A and before B, and after the execution of B (Fig. 2).
Sequential composition of services A and B
Figure 2: Sequential composition of services A and B. Information routed inside A and B is explicitly represented.

The semantics of the sequential composition would be
∀x ∃z ·((PA(x, a) ⇒ QA(x, z, b)) ∧ (PB(z, b) ⇒ ∃y ·QB(z, y, c)))
(1)
From Eq. (1) we can deduce:
∀x ∃z ·(PA(x, a) ∧PB(z, b) ⇒ ∃y ·(QA(x, z, b) ∧QB(z, y, c)))
(2)
However, Eq. (2) exposes internal variable z to the precondition. This is not desirable, since preconditions should be externally checkable and depend only on the input data to the composition. We can use the postcondition of A to eliminate this shortcoming:
∀x ∃z ·(PA(x, a) ∧QA(x, z, b) ∧PB(z, b) ⇒ ∃y ·(QA(x, z, b) ∧QB(z, y, c)))
(3)
In Eq. (3) the precondition can be checked exclusively based on x.1
The derived specification shows what conditions must be met before executing the sequence A ; B and which conditions will hold after a successful execution. However, it does not state clearly which conditions must hold for the composition to be valid. For a sequential composition to be valid there should be at least one case where it is applicable: the precondition of the first service should hold and the precondition of the second one should be true when applied to the result of the first service. Expressed in FOL, this validity condition is as follows:
∃x, z, y · (PA(x) ∧QA(x, z, b) ⇒ PB(z, b))
(4)
Note that there is a close connection with Hoare's triples [14] (which we explore in more depth in Section V): in that formalism our notion of an empty domain would correspond to inferring a false precondition for a piece of code.

C.  AND-Split/AND-Join

In the AND-Split/AND-Join composition pattern, which we denote by A(x, z) ∧B(w, y), there are two (or more) diverging branches of activities that are executed concurrently. Eventually the two branches converge into one branch, but only after activities on both branches have completed successfully.
Parallel composition of services A and B
Figure 3: Parallel composition of services A and B

For the composite service of Fig. 3, if we consider the AND-Split/AND-Join case, the following holds:
∀x ·(PA(x, a) ⇒ ∃z ·QA(x, z, c)) ∧ ∀w ·(PB(w, b) ⇒ ∃y ·QB(w, y, d))
(5)
Note that it is possible for states a and b (and for states c and d as well) to be equivalent, but we leave equations in their general form. In a similar way to the sequential case, we can deduce from Eq. (5) the following:
∀x ∀w ·(PA(x, a) ∧PB(w, b) ⇒ ∃z, y ·(QA(x, z, c) ∧QB(w, y, d)))
(6)
In this case, there is no need for further steps, as all input and output variables should be externally visible. As far as the validity condition is concerned, we only need to ensure that there is a case where the preconditions of both services are true:
∃x, w · (PA(x, a) ∧PB(w, b))
(7)
The same validity condition applies to all parallel composition patterns. Now that we have derived specifications for the sequential and AND-Split/AND-Join composition patterns, we will attempt to apply the derivation to the motivating example. The parallel execution of services CheckRequest and CheckPayment, results in the following specification, based on Eq. (6):
∀request, payForm, user · (FilledIn(request,1) ∧FilledIn(payForm,1) ∧LoggedIn(user,1) ⇒ Valid(request,2) ∧Valid(payForm,2)
(8)
Here, we use the state identifiers included in Figure 1. For example, LoggedIn(user,1) is true if user is logged in before the execution of CheckRequest/CheckPayment. Given the above specification, we can now derive the specification for the composite service up to the ExecutePayment service, which is a sequence of 3 services: Login, CheckRequest/CheckPayment and ExecutePayment. The specification is derived by first producing the specification for the subsequence of the first 2 services, based on Eq. (2):
∀request, payForm, user ·
(Valid(user,0) ∧¬LoggedIn(user,0) ∧FilledIn(request,1) ∧FilledIn(payForm,1) ∧LoggedIn(user,1) ⇒
LoggedIn(user,1) ∧Valid(request,2)) ∧ Valid(payForm,2))
(9)
Notice that we use Eq. (2) instead of Eq. (3) because no internal variables are exposed. Adding the ExecutePayment service to the sequence, results in the following specification:
∀request, payForm, user ·
(Valid(user,0) ∧¬LoggedIn(user,0) ∧FilledIn(request,1) ∧FilledIn(payForm,1) ∧LoggedIn(user,1) ∧ Valid(payForm,2)) ⇒
LoggedIn(user,1) ∧Valid(request,2)) ∧ Valid(payForm,2)) ∧∃doc ·PayCompleted(doc, user,3))
(10)
Note that LoggedIn(user,1) and Valid(payForm,2) appear on both sides of the implication, and therefore can be removed from the right hand side without changing the meaning of the formula. This is an example of specification simplification, which will be discussed in Section  III-G.

D.  OR-Split/OR-Join

The OR-Split/OR-Join composition pattern, which we denote by A(x, z) ∨B(w, y), is similar to the AND-Split/AND-Join pattern but with two fundamental differences. First, not all of the diverging branches are necessarily activated. Instead, a mechanism selects one or more of them to be executed each time. Second, at the merging stage there is no need for synchronization between the converging branches.
For the composite service of Figure 3, if we consider the OR-Split/OR-Join case, the following holds:
∀x ·(PA(x, a) ⇒ ∃z ·QA(x, z, c)) ∨ ∀w ·(PB(w, b) ⇒ ∃y ·QB(w, y, d))
(11)
From Eq. (11), we can deduce the following:
∀x ∀w ·(PA(x, a) ∧PB(w, b) ⇒ ∃z, y ·(QA(x, z, c) ∨QB(w, y, d)))
(12)
As we mentioned previously, the validity condition is the same as in the AND-Split/AND-Join case (Eq. 7). Intuitively, the reason is that we do not know which branch is going to be executed, and therefore we must require that all of them are eligible. This validity condition may appear too strong for an OR (or XOR) parallelism, however it can't be weakened without any extra knowledge about the particular parallel execution. While this may lead us to label a composition as invalid, when eventually the branch that caused the invalidity is not executed, it guarantees that no invalid composition is mislabeled as valid, which is far more important.

E.  XOR-Split/XOR-Join

The XOR-Split/XOR-Join composition pattern, that can be denoted by A(x, z) ⊕B(w, y), differs from the previous pattern in that it allows only one of the diverging branches to be executed each time. Hence, when the branches converge, only one of the branches is expected to provide results.
For the composite service of Figure 3, if we consider the XOR-Split/XOR-Join case, the following holds:
∀x ·(PA(x, a) ⇒ ∃z ·QA(x, z, c)) ⊕ ∀w ·(PB(w, b) ⇒ ∃y ·QB(w, y, d))
(13)
XOR between two operands can be expressed as a conjunction of an OR between the operands and a negated AND between the same operands. Using the results of the calculations in the previous cases we result in Eq (14):
∀x, w ·(PA(x, a) ∧PB(w, b) ⇒ ∃z, y ·(QA(x, z, c) ∨QB(w, y, d)) ∧
¬(PA(x, a) ∧PB(w, b) ⇒ ∃z, y ·(QA(x, z, c) ∧QB(w, y, d)))
(14)
From Eq. (14), we can deduce the following:
∀x, w ·(PA(x, a) ∧PB(w, b) ⇒ ∃z, y ·(QA(x, z, c) ⊕QB(w, y, d)))
(15)
The validity condition is once again expressed by Eq. 7.

F.  Conditional Constructs

Conditional constructs, such as if-then-else or switch statements, evaluate a condition in order to decide which branch will be executed. Similarly to the XOR-Split/XOR-Join pattern, only one of the branches is selected, based on the truth value of the condition.
Conditional composition of services A and B
Figure 4: Conditional composition of services A and B

In an if-then-else composition of the form IF C(x) THEN A(x, y) ELSE B(x, y), as seen in Figure 4, if the condition C is true, then this implies that A is executed; if the condition is false, then this implies that B is executed. Input variable x refers to either of the two services since the branches are exclusive and the same is true for output variable y. x also contains the terms that are involved in the condition C. Hence, the following should hold:

∀x ·(C(x, e) ⇒ ∃y ·(PA(x, a) ⇒ QA(x, y, c)))∧
(¬C(x, e) ⇒ ∃y ·(PB(x, b) ⇒ QB(x, y, d)))
(16)
From Eq. (16), we can deduce the following:

∀x ∃y · ([(C(x, e) ∧PA(x, a)) ∨(¬C(x, e) ∧PB(x, b))] ⇒
([(C(x, e) ∧QA(x, y, c)) ∨(¬C(x, e) ∧QB(x, y, d))]))
(17)
Determining whether a conditional composition is valid depends on finding a case where the precondition derived above is valid, resulting in the following validity check:

∃x · ((C(x, e) ∧PA(x, a)) ∨(¬C(x, e) ∧PB(x, b)))
(18)
We can now return and complete the specification for our example, by deriving first the specification for the conditional execution of CreateCertified and CreateUncertified based on Eq. (17) and given the condition ReqCertif(doc, user, 3):
∀doc, user, ∃certifDoc · ([(ReqCertif(doc, user, 3) ∧ PayCompleted(doc, user, 4))∨ (¬ReqCertif(doc, user, 3) ∧ PayCompleted(doc, user, 5))]
⇒ [(ReqCertif(doc, user, 3) ∧ CertifCompleted(doc, user, 6) ∧ Delivered(certifDoc, user, 6)) ∨
(¬ReqCertif(doc, user, 3) ∧ Delivered(doc, user, 6))])
(19)
Given that specification and the one we derived earlier for the rest of the composition (Eq. (10)) and applying the derivation actions for a sequence, we result in the following complete specification for the composite process of our example:
∀request, payForm, doc, user, ∃certifDoc ·
(Valid(user,0) ∧¬LoggedIn(user,0) ∧FilledIn(request,1) ∧FilledIn(payForm,1) ∧LoggedIn(user,1) ∧Valid(payForm,2)
[(ReqCertif(doc, user, 3) ∧ PayCompleted(doc, user, 4))∨ (¬ReqCertif(doc, user, 3) ∧ PayCompleted(doc, user, 5))]
⇒ (LoggedIn(user,1) ∧Valid(request,2) ∧Valid(payForm,2) ∧PayCompleted(doc, user,3)
∧[(ReqCertif(doc, user, 3) ∧ CertifCompleted(doc, user, 6) ∧Delivered(certifDoc, user, 6)) ∨
(¬ReqCertif(doc, user, 3) ∧ Delivered(doc, user, 6))]))
(20)
Table II shows the derived preconditions and postconditions for the basic constructs that we examined in this Section.
Construct PreconditionPostcondition
Sequence PA(x, a) ∧QA(x, z, b) ∧PB(z, b) QA(x, z, b) ∧QB(z, y, c)
AND-Split/Join PA(x, a) ∧PB(w, b) QA(x, z, c) ∧QB(w, y, d)
OR-Split/Join PA(x, a) ∧PB(w, b) QA(x, z, c) ∨QB(w, y, d)
XOR-Split/Join PA(x, a) ∧PB(w, b) QA(x, z, c) ⊕QB(w, y, d)
Conditional (C(u, e) ∧PA(x, a)) ∨(¬C(u, e) ∧PB(x, b)) (C(u, e) ∧QA(x, y, c)) ∨ (¬C(u, e) ∧QB(x, y, d))
Table 2: Derived preconditions and postconditions

G.  Simplifying the Derived Specification

As compositions become larger and more complicated, both with regard to the number of services and the composition schema, the derived specification will, in turn, grow similarly. This should have become obvious through the motivating example, where the final specification can be considered large, although still easily processable by a theorem prover. In even more complex composite services, the need to somehow simplify and compact the resulting specification becomes more crucial, demanding the formulation of a simplification process that should follow the derivation.
Simplifying a specification involves a series of tasks, ranging from generic ones such as dealing with duplicate predicates (for instance, predicates that appear in both sides of an implication, as mentioned at the end of Section III-C) and applying known equivalences, to tasks that depend on specific knowledge on the particular composite service. For instance, in the final specification as expressed in Eq. (20), the precondition:

(ReqCertif(doc, user, 3) ∧ PayCompleted(doc, user, 4)) ∨ (¬ReqCertif(doc, user, 3) ∧ PayCompleted(doc, user, 5))
under the monotonicity constraint that once a payment process is completed, it remains completed thereafter (which comes from domain knowledge)
∀x ∃y ·(y > x) ∧ Valid(payForm, x) ⇒ PayCompleted(doc, user, y)
is equivalent to PayCompleted(doc, user, 4), which is reasonable due to the nature of the preconditions of the services that form the if-then-else part of the composition and the equivalence of states 4 and 5.

IV.  Handling Loops and Asynchronous Execution

The loop structure was excluded from the discussion in Section III. Loops allow for the repeated execution of a task or a process until a condition (the loop guard) ceases to hold. This poses a significant challenge as there is no a priori knowledge of how many iterations will be performed. Due to that fact, the state identifiers that we used in all other constructs to differentiate predicate evaluations are rendered inapplicable.
Without knowledge of its precondition and postcondition, a possible way to specify a loop is by formulating the specification based on an upper limit on the number of iterations. For a looped execution under condition C and for a maximum number of k iterations, knowing that the looped commands are specified by preconditions P(x) and Q(x, y), where x and y are the input and output variables, yields the following recursive loop specification:
L(x,x′,0) ⇐ (¬C(x) ∧x=x′) ∧
L(x,x′,k) ⇐ k > 0 ∧C(x) ∧(P(x) ⇒ Q(x,y)) ∧L(y,x′,k−1)
(21)
L(x,x′,k) denotes the k-th iteration of a loop with input variables x and output variables x′. Recursive specifications like (Eq. 21), while rather expressive and concise, are difficult to work with, especially by theorem provers. Also, such a specification wouldn't be useful as part of a service specification, particularly in the case of asynchronous interaction, discussed later in this Section. Moreover, it depends on the ability to determine ahead of time an upper limit on the number of iterations, which cannot be expected to be always available.
Without knowledge of an upper limit on the number of iterations, a means to characterize a loop is through its invariant. A loop invariant I is a statement that is true before and after each iteration of the loop, thus it stays unaffected by the loop execution. By definition, the loop invariant is a loop precondition (I ⇒ P). Moreover, a loop postcondition can be derived through the following implication: I ∧¬C ⇒ Q, where C is the loop guard, the condition that must be true for the iteration to continue [15].
Several issues are raised in the discussion of using invariants to generate loop specifications. A fundamental one is which of the possible statements that may be produced by a loop invariant generation process is the most suitable choice. The selected loop invariant should be at least strong enough to imply a successful execution of the loop if it was limited to a single iteration. For instance, if P1 ⇒ Q1 describes the successful execution of the looped services for a single iteration, then we need the loop invariant to be at least strong enough so that I ⇒ P1 and I ∧¬C ⇒ Q1 hold.

A.  Generating Loop Invariants

As far as the loop invariant generation process is concerned, we once again have to consider the special characteristics of the service-oriented world. In the traditional programming languages case, generating invariants is based on the commands that form the body of the loop, whereas in the services case, we can only rely on an approximate specification of the body. Hence, we can expect that a generated invariant is an approximation too. The correct direction of the approximation needs to be determined.
Suppose that we have an invariant Iw that is a weaker safe approximation of the invariant I that would be generated based on the actual code of the loop, i.e. I ⇒ Iw. If we use that invariant as a precondition, then we may allow invalid executions, which is unacceptable. On the other hand, if we use it to derive a postcondition Qw by applying the implication Iw ∧¬C ⇒ Qw, then Q ⇒ Qw, meaning that we will get a weaker postcondition, which is acceptable, since the specified results of the execution are more than the actual ones.
Suppose now that we have an invariant Is that is a stronger safe approximation of I, i.e. Is ⇒ I. This will lead to a stronger precondition, which is what we expect from an approximate specification of a service, but also a stronger postcondition (if Is ∧¬C ⇒ Qs, then Qs ⇒ Q), which is problematic, because some of the actual results of the service may not be specified. Consequently, we need a stronger approximation of the invariant in order to derive a useful precondition, and a weaker approximation in order to derive a useful postcondition.
Another issue concerning invariant generation is the peculiar characteristics of our case. While, in general, invariant generation is based on a set of commands (the loop program), in our case we only have an approximate specification of the commands of the loop, so the generation process must be based on this information. Essentially, the invariant generator must take into account the preconditions of the looped commands, so that the resulting invariant at least implies these preconditions, as mentioned at the beginning of this section.
Furia and Meyer [16] provide a concise summary on the different methods that have been proposed in literature to generate loop invariants. Of the works mentioned, only static methods that do not depend on executing the program and do not rely on existing program annotations can be applied in our case since we actually need the invariant as a means to specify the loop and not the other way round. Methods such as abstract interpretation [17,18,19,20] and constraint-based techniques [21,22] are applicable, although they should be adapted in order to take into account the discussion in this section.

B.  Specifying Asynchronous Services

So far, we have made the implicit assumption that all service executions are synchronous: a service receives a request, the client waits for the service to handle the request and the service returns a response. However, it is very common in Service-Oriented Computing to employ services that interact in an asynchronous manner: the client invokes the service but does not wait for the response, which may take more time to be produced than in the synchronous case. It is important to determine how this asynchronous interaction affects the derivation process we have described so far.
As far as preconditions are concerned, there is no difference: whether it is a synchronous or an asynchronous interaction, preconditions need to be true at the moment the request is received. However, the evaluation of postconditions is affected, because in the asynchronous case the response is received in a state which may differ from that in which the invocation was performed. Hence, care must be taken to ensure that postconditions are expressed and evaluated in the correct context.
In order to deal with this issue, we borrow the property of Static Single Assignment form (SSA) [23] from compiler design. SSA states that there is exactly one assignment for each distinct variable in a program. To implement assignments to the same variable, variable renaming is employed, so that if, for instance, a variable y is involved in two assignments, it is renamed to y1 and y2.
Let's return to the motivating example. Suppose that the ExecutePayment service is executed asynchronously. This means that after checking the precondition and invoking the service, the composite process continues to the certification phase. Let's assume that we have a more detailed version of the precondition, Valid(payForm, user, si), which is true when the particular user has correctly filled in the corresponding payment form. If, after the invocation of ExecutePayment, another service has to modify the variable user, it is renamed to user1. Thus, when the asynchronous service completes execution and the postcondition PayCompleted(doc, user,so) has to be checked, it will be evaluated against the value of variable user that matches the value used in the evaluation of the precondition.
In the case of loops, expressing specifications using the SSA form requires that we know an upper limit for the number of iterations, otherwise it is not possible to apply the variable renaming scheme. In absence of such an upper limit, loop specification derivation must follow the detailed discussion in this section, in order to produce simpler specifications for which SSA can be easily applied.

V.  Related Work

Formal specifications have been used in computer science in order to describe what a system should do. Specifications can be used to drive the system's implementation and to verify whether existing systems (or design plans) are correct with respect to the specification that was agreed upon. A traditional format of a program specification contains the conditions that should be met prior to execution (called preconditions) and the conditions that result after a successful execution of the program (called postconditions or results). Hoare [14] introduced the well-known triple notation P {S} Q which expresses that if preconditions P are met before initiating execution of program S, then when the execution completes postconditions Q will be true.
Hoare's notation expresses a sufficient set of conditions for a program to have a desired set of results. Dijkstra [6] expanded on this by focusing on necessary and sufficient (called weakest) preconditions, that also guarantee the desired result. The notation he introduced, wp(S, Q) denotes the weakest precondition for program S, which is "the set of all states such that execution of S begun in anyone of them is guaranteed to terminate in a finite amount of time in a state satisfying Q" [15]. Dijkstra then defined the weakest preconditions for basic statements such as assignment, conditionals, or loops and showed that one can derive formally a set of statements that, if executed, will lead to a specified result, by using structural induction on the basic weakest preconditions.
Our work attempts to bring Dijkstra's derivation of program specifications in the field of Service-Oriented Computing, hence it differs in some important points. The defining difference is that Dijkstra's derivation process is driven by the program implementation. In the case of services, we have no access to the implementation, thus we cannot use it to either drive the derivation process or verify the resulting specification. Another important difference is that the weakest precondition derivation relies on specifications that aren't approximations: in order to derive the weakest precondition for a composition using the wp operator, we need to have the weakest preconditions for all participating services. As we have already mentioned, service specifications are most often approximations and as a result, they cannot be used in combination with the wp operator. Finally, a further differentiating point in comparison to programming specifications is the asynchronous interaction that we encounter in services, which is not addressed in programming specifications.
Despite the differences outlined above, it is important to make sure that our approach does not contradict Dijkstra's. In other words, we need to ensure that our approach does not infer a precondition that is weaker than the one calculated by the wp operator. We now provide an intuitive explanation supporting this for the case of the sequential composition. Let us reason by contradiction and assume that the precondition produced by our approach, P, is not stronger or as strong as the weakest precondition Pwp: ¬(P ⇒ Pwp) - or, equivalently, P ∧¬Pwp , i.e., there are states in which the weakest precondition Pwp does not hold, but in which our precondition P holds, which by definition makes P incorrect.
Since the initial assumption is that P ∧¬Pwp is true, then PA ∧PB ∧¬Pwp must also be true. From the discussion at the beginning of Section III, we know that the approximated preconditions PA and PB are stronger than or equivalent to the corresponding weakest preconditions PwpA and PwpB, i.e., PA ⇒ PwpA and PB ⇒ PwpB. With that into account, we need PwpA ∧PwpB ∧¬Pwp to be true.
The result is contradictory since we want at the same time the precondition of a composite service to be false and the preconditions of the services it contains to be true. In particular, the precondition of the leftmost service, PA, has to be true, since it is the "starting point" of the composition. Hence our assumption was incorrect, meaning that our approach will never produce a precondition that is weakest than the one derived by the wp operator. In a similar manner, we can prove that our result holds for all control constructs handled in this work, since in almost all of them, P contains the conjunction of PA and PB. The only exception is the conditional case, where the derived precondition contains a disjunction of PA and PB, depending on the condition truth value. Regardless, the contradiction we have proven still holds, since in any case either PA or PB will have to be true.
Another work related to specification derivation is that of Ghezzi et al. [24,25] which focuses on methods for specification recovery.  [24] proposes a method to infer algebraic specifications of abstract data types, given the related class and its methods and with no access to the source code. Behavior models are extracted based on the run-time behavior of the class to be specified and are used to drive the generation and selection of possible actions performed by the class, described as terms, i.e. sequences of legal method applications with fixed actual parameters, starting from a constructor.  [25] similarly creates behavior models by observing the input-output relationships after executing the methods of the class. Then, graph transformation rules are applied in order to result in a generalization of the initial behavior models, which is the inferred specification for the class. These works rely on the run-time behavior of a component in order to derive its specification, which is different from our approach, in which we rely on the specifications of sub-components and the control flow between them.

VI.  Conclusions and Future Work

In this paper, we proposed an approach for inferring composite service specifications given the specifications of the services participating in the composition (in the form of sets of preconditions and postconditions) and the composition schema. The approach attempts to construct the specification by using structural induction based on derivation rules defined for most fundamental control constructs. The resulting specification can be used to formally describe the composite service in terms of its preconditions and postconditions without requiring any knowledge of the internals of the composition, allowing for an actual "black box" view of the whole process.
The nature of the proposed approach facilitates a possible implementation: structural induction lends itself to be written as a recursive algorithm. Hence, it would be straightforward to create an automated process that takes a set of service specifications and a composition schema and produces the specification for the composite service of the schema. Such specifications can then be used to prove desired properties of the composite service or be fed to automated composition approaches that accept preconditions and postconditions as input [26].
Future work includes implementing the proposed approach and evaluating it for compositions of varying complexity. Concerning specification simplification, we plan to look into the work of Douglas Smith [27] on simplifying precondition formulas and determine whether the actions he proposes may be applied in our case. Finally, it would be interesting to explore whether the resulting specifications suffer from the frame problem and related issues as examined in [28].

Acknowledgments

The research leading to these results has received funding from the European Community's Seventh Framework Programme FP7/2007-2013 under grant agreement 215483 (S-Cube). Manuel Carro has also been partially funded by Spanish MICINN project TIN-2008-05624 DOVES and CAM project S2009TIC-1465 PROMETIDOS.

References

[1]
S. Benbernou, L. Cavallaro, M. S. Hacid, R. Kazhamiakin, G. Kecskemeti, J.-L. Pazat, F. Silvestri, M. Uhlig, and B. Wetzstein, "PO-JRA-1.2.1: State of the Art Report, Gap Analysis of Knowledge on Principles, Techniques and Methodologies for Monitoring and Adaptation of SBAs," S-Cube Network of Excellence, Tech. Rep., July 2008. [Online]. Available: http://www.s-cube-network.eu/results/deliverables/wp-jra-1.2/
[2]
C. B. Jones, Systematic Software Development Using VDM, 2nd ed., ser. International Series in Computer Science.    Upper Saddle River, NJ, USA: Prentice-Hall, Inc., 1991.
[3]
J. M. Spivey, The Z notation: a reference manual.    Upper Saddle River, NJ, USA: Prentice-Hall, Inc., 1989.
[4]
J. R. Abrial, The B-book: assigning programs to meanings.    The Pitt Building, Trumpington Street, Cambridge CB2 1RP: Cambridge University Press, 1996.
[5]
J.-R. Abrial, Modeling in Event-B.    Cambridge University Press, May 2010.
[6]
E. W. Dijkstra, "Guarded commands, nondeterminacy and formal derivation of programs," Communications of the ACM, vol. Volume 18 , Issue 8, pp. 453-457, August 1975.
[7]
2 plus 43 minus 4 E. D. Nitto, V. Mazza, and A. Mocci, "CD-IA-2.2.2: Collection of industrial best practices, scenarios and business cases," S-Cube Network of Excellence, Tech. Rep., May 2009. [Online]. Available: http://www.s-cube-network.eu/results/deliverables/wp-ia-2.2/
[8]
J. Mendling, K. B. Lasse, and U. Zdun, "On the transformation of control flow between block-oriented and graph-oriented process modelling languages," International Journal of Business Process Integration and Management, vol. 3, no. 2, pp. 96-108, 2008.
[9]
R. A. Kowalski, Logic for Problem Solving.    Elsevier North-Holland Inc., 1979.
[10]
M. Shanahan, Solving the Frame Problem: A Mathematical Investigation of the Common Sense Law of Inertia.    MIT Press, 1997.
[11]
W. McCune, "Prover9 and Mace4," 2005-2010, http://www.cs.unm.edu/ mccune/prover9/.
[12]
2 plus 43 minus 4 W. van der Aalst, A. ter Hofstede, B. Kiepuszewski, and A. Barros, "Workflow patterns," Distributed and Parallel Databases, vol. 14, no. 1, pp. 5-51, 2003. [Online]. Available: http://dx.doi.org/10.1023/A:1022883727209
[13]
2 plus 43 minus 4 N. Russell, A. ter Hofstede, W. van der Aalst, and N. Mulyar, "Workflow control-flow patterns: A revised view," BPM Center, Tech. Rep. BPM-06-22, June 2006. [Online]. Available: http://workflowpatterns.com/documentation/documents/BPM-06-22.pdf
[14]
C. A. R. Hoare, "An Axiomatic Basis for Computer Programming," Comm. ACM, vol. 12, no. 10, pp. 576-580, 583, October 1969.
[15]
D. Gries, The Science of Programming.    Springer, 1981.
[16]
2 plus 43 minus 4 C. A. Furia and B. Meyer, "Inferring loop invariants using postconditions," CoRR, vol. abs/0909.0884, 2009. [Online]. Available: http://dblp.uni-trier.de/db/journals/corr/corr0909.html#abs-0909-0884
[17]
2 plus 43 minus 4 P. Cousot and R. Cousot, "Abstract interpretation: A unified lattice model for static analysis of programs by construction or approximation of fixpoints." in POPL '77: Proceedings of the 4th ACM SIGACT-SIGPLAN symposium on Principles of programming languages.    ACM Press, 1977, pp. 238-252. [Online]. Available: http://doi.acm.org/10.1145/512950.512973
[18]
F. Logozzo, "Automatic inference of class invariants." in VMCAI, ser. Lecture Notes in Computer Science, B. Steffen and G. Levi, Eds., vol. 2937.    Springer, 2004, pp. 211-222.
[19]
B.-Y. E. Chang and K. R. M. Leino, "Abstract interpretation with alien expressions and heap structures." in VMCAI, ser. Lecture Notes in Computer Science, R. Cousot, Ed., vol. 3385.    Springer, 2005, pp. 147-163.
[20]
2 plus 43 minus 4 E. Rodríguez-Carbonell and D. Kapur, "Automatic Generation of Polynomial Invariants of Bounded Degree Using Abstract Interpretation," Science of Computer Programming, vol. 64, no. 1, pp. 54 - 75, 2007, special issue on the 11th Static Analysis Symposium - SAS 2004. [Online]. Available: http://www.sciencedirect.com/science/article/B6V17-4M0J4BD-1/2/017d8305a94fbc772b9bf92c12f96dba
[21]
M. Colón, S. Sankaranarayanan, and H. Sipma, "Linear invariant generation using non-linear constraint solving," in CAV, ser. LNCS, vol. 2725.    Springer, July 2003, pp. 420-433.
[22]
S. Sankaranarayanan, H. Sipma, and Z. Manna, "Non-linear loop invariant generation using Gröbner bases," in ACM Principles of Programming Languages (POPL).    ACM Press, 2004, pp. 318-330.
[23]
B. K. Rosen, M. N. Wegman, and F. K. Zadeck, "Global value numbers and redundant computations," in Proceedings of the 15th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, 1988, pp. 12-27.
[24]
C. Ghezzi, A. Mocci, and M. Monga, "Efficient recovery of algebraic specifications for stateful components," in IWPSE, 2007, pp. 98-105.
[25]
--, "Synthesizing intensional behavior models by graph transformation," in ICSE, 2009, pp. 430-440.
[26]
2 plus 43 minus 4 P. Bartalos and M. Bielikova, "Qos aware semantic web service composition approach considering pre/postconditions." in ICWS.    IEEE Computer Society, 2010, pp. 345-352. [Online]. Available: http://dblp.uni-trier.de/db/conf/icws/icws2010.html#BartalosB10
[27]
2 plus 43 minus 4 D. R. Smith, "Derived preconditions and their use in program synthesis." in CADE, ser. Lecture Notes in Computer Science, D. W. Loveland, Ed., vol. 138.    Springer, 1982, pp. 172-193. [Online]. Available: http://dblp.uni-trier.de/db/conf/cade/cade82.html#Smith82
[28]
2 plus 43 minus 4 G. Baryannis and D. Plexousakis, "The frame problem in web service specifications," in Proceedings of the 2009 ICSE Workshop on Principles of Engineering Service Oriented Systems, ser. PESOS '09.    Washington, DC, USA: IEEE Computer Society, 2009, pp. 9-12. [Online]. Available: http://dx.doi.org/10.1109/PESOS.2009.5068813

Footnotes:

1All proofs in this paper were checked using the Prover9 [11] theorem prover. The corresponding files can be found online here

File partially translated from TEX by TTH, version 4.03.